Trimmed estimator

Last updated July 05, 2022

In statistics, a trimmed estimator is an estimator derived from another estimator by excluding some of the extreme values, a process called truncation. This is generally done to obtain a more robust statistic, and the extreme values are considered outliers.^[1] Trimmed estimators also often have higher efficiency for mixture distributions and heavy-tailed distributions than the corresponding untrimmed estimator, at the cost of lower efficiency for other distributions, such as the normal distribution.

Given an estimator, the x% trimmed version is obtained by discarding the x% lowest or highest observations or on both end: it is a statistic on the middle of the data. For instance, the 5% trimmed mean is obtained by taking the mean of the 5% to 95% range. In some cases a trimmed estimator discards a fixed number of points (such as maximum and minimum) instead of a percentage.

Examples

The median is the most trimmed statistic (nominally 50%), as it discards all but the most central data, and equals the fully trimmed mean – or indeed fully trimmed mid-range, or (for odd-size data sets) the fully trimmed maximum or minimum. Likewise, no degree of trimming has any effect on the median – a trimmed median is the median – because trimming always excludes an equal number of the lowest and highest values.

Quantiles can be thought of as trimmed maxima or minima: for instance, the 5th percentile is the 5% trimmed minimum.

Trimmed estimators used to estimate a location parameter include:

Trimmed mean
Modified mean, discarding the minimum and maximum values
Interquartile mean, the 25% trimmed mean
Midhinge, the 25% trimmed mid-range

Trimmed estimators used to estimate a scale parameter include:

Interquartile range, the 25% trimmed range
Interdecile range, the 10% trimmed range

Trimmed estimators involving only linear combinations of points are examples of L-estimators.

Applications

Estimation

Most often, trimmed estimators are used for parameter estimation of the same parameter as the untrimmed estimator. In some cases the estimator can be used directly, while in other cases it must be adjusted to yield an unbiased consistent estimator.

For example, when estimating a location parameter for a symmetric distribution, a trimmed estimator will be unbiased (assuming the original estimator was unbiased), as it removes the same amount above and below. However, if the distribution has skew, trimmed estimators will generally be biased and require adjustment. For example, in a skewed distribution, the nonparametric skew (and Pearson's skewness coefficients) measure the bias of the median as an estimator of the mean.

When estimating a scale parameter, using a trimmed estimator as a robust measures of scale, such as to estimate the population variance or population standard deviation, one generally must multiply by a scale factor to make it an unbiased consistent estimator; see scale parameter: estimation.

For example, dividing the IQR by $2{\sqrt {2}}\operatorname {erf} ^{-1}(1/2)\approx 1.349$ (using the error function) makes it an unbiased, consistent estimator for the population standard deviation if the data follow a normal distribution.

Other uses

Trimmed estimators can also be used as statistics in their own right – for example, the median is a measure of location, and the IQR is a measure of dispersion. In these cases, the sample statistics can act as estimators of their own expected value. For example, the MAD of a sample from a standard Cauchy distribution is an estimator of the population MAD, which in this case is 1, whereas the population variance does not exist.

Related Research Articles

In statistics, a central tendency is a central or typical value for a probability distribution.

In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule, the quantity of interest and its result are distinguished. For example, the sample mean is a commonly used estimator of the population mean.

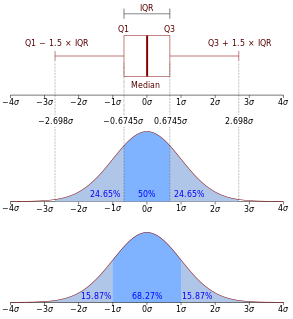
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the difference between the 75th and 25th percentiles of the data. To calculate the IQR, the data set is divided into quartiles, or four rank-ordered even parts via linear interpolation. These quartiles are denoted by Q₁ (also called the lower quartile), Q₂ (the median), and Q₃ (also called the upper quartile). The lower quartile corresponds with the 25th percentile and the upper quartile corresponds with the 75th percentile, so IQR = Q₃ − Q₁_.

In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as "the middle" value. The basic feature of the median in describing data compared to the mean is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a "typical" value. Median income, for example, may be a better way to suggest what a "typical" income is, because income distribution can be very skewed. The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data are contaminated, the median is not an arbitrarily large or small result.

A statistic (singular) or sample statistic is any quantity computed from values in a sample which is considered for a statistical purpose. Statistical purposes include estimating a population parameter, describing a sample, or evaluating a hypothesis. The average of sample values is a statistic. The term statistic is used both for the function and for the value of the function on a given sample. When a statistic is being used for a specific purpose, it may be referred to by a name indicating its purpose.

In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.

Skewness Measure of the asymmetry of random variables

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.

In statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter. More formally, it is the application of a point estimator to the data to obtain a point estimate.

In descriptive statistics, a box plot or boxplot is a method for graphically demonstrating the locality, spread and skewness groups of numerical data through their quartiles. In addition to the box on a box plot, there can be lines extending from the box indicating variability outside the upper and lower quartiles, thus, the plot is also termed as the box-and-whisker plot and the box-and-whisker diagram. Outliers that differ significantly from the rest of the dataset may be plotted as individual points beyond the whiskers on the box-plot. Box plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying statistical distribution. The spacings in each subsection of the box-plot indicate the degree of dispersion (spread) and skewness of the data, which are usually described using the five-number summary. In addition, the box-plot allows one to visually estimate various L-estimators, notably the interquartile range, midhinge, range, mid-range, and trimean. Box plots can be drawn either horizontally or vertically.

The average absolute deviation (AAD) of a data set is the average of the absolute deviations from a central point. It is a summary statistic of statistical dispersion or variability. In the general form, the central point can be a mean, median, mode, or the result of any other measure of central tendency or any reference value related to the given data set. AAD includes the mean absolute deviation and the median absolute deviation.

A truncated mean or trimmed mean is a statistical measure of central tendency, much like the mean and median. It involves the calculation of the mean after discarding given parts of a probability distribution or sample at the high and low end, and typically discarding an equal amount of both. This number of points to be discarded is usually given as a percentage of the total number of points, but may also be given as a fixed number of points.

This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.

In statistics, the mid-range or mid-extreme is a measure of central tendency of a sample (statistics) defined as the arithmetic mean of the maximum and minimum values of the data set:

Robust statistics is statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normal. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard-deviations; under this model, non-robust methods like a t-test work poorly.

In statistics, the bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. In statistics, "bias" is an objective property of an estimator. Bias can also be measured with respect to the median, rather than the mean, in which case one distinguishes median-unbiased from the usual mean-unbiasedness property. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased; see bias versus consistency for more.

In statistical theory, a U-statistic is a class of statistics that is especially important in estimation theory; the letter "U" stands for unbiased. In elementary statistics, U-statistics arise naturally in producing minimum-variance unbiased estimators.

In statistics, an L-estimator is an estimator which is a linear combination of order statistics of the measurements. This can be as little as a single point, as in the median, or as many as all points, as in the mean.

In statistics, robust measures of scale are methods that quantify the statistical dispersion in a sample of numerical data while resisting outliers. The most common such robust statistics are the interquartile range (IQR) and the median absolute deviation (MAD). These are contrasted with conventional or non-robust measures of scale, such as sample variance or standard deviation, which are greatly influenced by outliers.

In statistics, dispersion is the extent to which a distribution is stretched or squeezed. Common examples of measures of statistical dispersion are the variance, standard deviation, and interquartile range. For instance, when the variance of data in a set is large, the data is widely scattered. On the other hand, when the variance is small, the data in the set is clustered.

In the comparison of various statistical procedures, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator, experiment, or test needs fewer observations than a less efficient one to achieve a given error performance. An efficient estimator is characterized by a small variance or mean square error, indicating that there is a small deviance between the estimated value and the "true" value.

References

↑ Kaltenbach, Hans-Michael (2012). A concise guide to statistics. Heidelberg: Springer. ISBN 978-3-642-23502-3. OCLC 763157853.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Kaltenbach, Hans-Michael (2012). A concise guide to statistics. Heidelberg: Springer. ISBN 978-3-642-23502-3. OCLC 763157853.

[1]