In mathematics, a continuous function is a function such that a continuous variation of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as discontinuities. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is not continuous. Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity.

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order."

A random variable is a mathematical formalization of a quantity or object which depends on random events.

In mathematics, a monotonic function is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.
In mathematics, fuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. At the same time, Salii (1965) defined a more general kind of structure called an L-relation, which he studied in an abstract algebraic context. Fuzzy relations, which are now used throughout fuzzy mathematics and have applications in areas such as linguistics, decision-making, and clustering, are special cases of L-relations when L is the unit interval [0, 1].

The sorites paradox is a paradox that results from vague predicates. A typical formulation involves a heap of sand, from which grains are removed individually. With the assumption that removing a single grain does not cause a heap to become a non-heap, the paradox is to consider what happens when the process is repeated enough times that only one grain remains: is it still a heap? If not, when did it change from a heap to a non-heap?
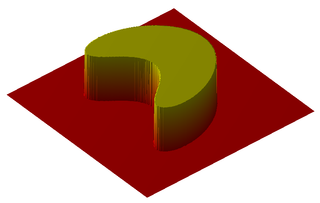
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements of the set to zero. The indicator function of a subset A of a set X maps X to the two-element set if an element in X belongs to A, and if does not belong to A. It may be denoted as by or by

In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of the function does not lie below the graph between the two points. Equivalently, a function is convex if its epigraph is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function and the exponential function . In simple terms, a convex function refers to a function whose graph is shaped like a cup , while a concave function's graph is shaped like a cap .
In mathematics, nonstandard calculus is the modern application of infinitesimals, in the sense of nonstandard analysis, to infinitesimal calculus. It provides a rigorous justification for some arguments in calculus that were previously considered merely heuristic.
In computer science, a rough set, first described by Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set. In the standard version of rough set theory, the lower- and upper-approximation sets are crisp sets, but in other variations, the approximating sets may be fuzzy sets.
In mathematics, the membership function of a fuzzy set is a generalization of the indicator function for classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition. Membership functions were introduced by Zadeh in the first paper on fuzzy sets (1965). Zadeh, in his theory of fuzzy sets, proposed using a membership function operating on the domain of all possible values.
In mathematics, a t-norm is a kind of binary operation used in the framework of probabilistic metric spaces and in multi-valued logic, specifically in fuzzy logic. A t-norm generalizes intersection in a lattice and conjunction in logic. The name triangular norm refers to the fact that in the framework of probabilistic metric spaces t-norms are used to generalize the triangle inequality of ordinary metric spaces.

Interval arithmetic is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable, mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of estimating the height of someone as exactly 2.0 metres, using interval arithmetic one might be certain that that person is somewhere between 1.97 and 2.03 metres.
In mathematical logic, a Boolean-valued model is a generalization of the ordinary Tarskian notion of structure from model theory. In a Boolean-valued model, the truth values of propositions are not limited to "true" and "false", but instead take values in some fixed complete Boolean algebra.
In mathematical logic, monoidal t-norm based logic, the logic of left-continuous t-norms, is one of the t-norm fuzzy logics. It belongs to the broader class of substructural logics, or logics of residuated lattices; it extends the logic of commutative bounded integral residuated lattices by the axiom of prelinearity.
T-norm fuzzy logics are a family of non-classical logics, informally delimited by having a semantics that takes the real unit interval [0, 1] for the system of truth values and functions called t-norms for permissible interpretations of conjunction. They are mainly used in applied fuzzy logic and fuzzy set theory as a theoretical basis for approximate reasoning.
In applied mathematics – specifically in fuzzy logic – the ordered weighted averaging (OWA) operators provide a parameterized class of mean type aggregation operators. They were introduced by Ronald R. Yager. Many notable mean operators such as the max, arithmetic average, median and min, are members of this class. They have been widely used in computational intelligence because of their ability to model linguistically expressed aggregation instructions.
A confidence band is used in statistical analysis to represent the uncertainty in an estimate of a curve or function based on limited or noisy data. Similarly, a prediction band is used to represent the uncertainty about the value of a new data-point on the curve, but subject to noise. Confidence and prediction bands are often used as part of the graphical presentation of results of a regression analysis.
In measurements, the measurement obtained can suffer from two types of uncertainties. The first is the random uncertainty which is due to the noise in the process and the measurement. The second contribution is due to the systematic uncertainty which may be present in the measuring instrument. Systematic errors, if detected, can be easily compensated as they are usually constant throughout the measurement process as long as the measuring instrument and the measurement process are not changed. But it can not be accurately known while using the instrument if there is a systematic error and if there is, how much? Hence, systematic uncertainty could be considered as a contribution of a fuzzy nature.














