
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are vector quantities. The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes:

A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In the theory of Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In physics, the Coriolis force is an inertial force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.

In physics, jerk (also known as jolt) is the rate of change of an object's acceleration over time. It is a vector quantity (having both magnitude and direction). Jerk is most commonly denoted by the symbol j and expressed in m/s3 (SI units) or standard gravities per second (g0/s).
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
In continuum mechanics, the Froude number is a dimensionless number defined as the ratio of the flow inertia to the external field. The Froude number is based on the speed–length ratio which he defined as:

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.
A banked turn is a turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn. For a road or railroad this is usually due to the roadbed having a transverse down-slope towards the inside of the curve. The bank angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the horizontal.

A transition curve is a spiral-shaped length of highway or railroad track that is used between sections having different profiles and radii, such as between straightaways (tangents) and curves, or between two different curves.
In atmospheric science, balanced flow is an idealisation of atmospheric motion. The idealisation consists in considering the behaviour of one isolated parcel of air having constant density, its motion on a horizontal plane subject to selected forces acting on it and, finally, steady-state conditions.
The Dean number (De) is a dimensionless group in fluid mechanics, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean, who was the first to provide a theoretical solution of the fluid motion through curved pipes for laminar flow by using a perturbation procedure from a Poiseuille flow in a straight pipe to a flow in a pipe with very small curvature.

In railway engineering, curve resistance is a part of train resistance, namely the additional rolling resistance a train must overcome when travelling on a curved section of track. Curve resistance is typically measured in per mille, with the correct physical unit being Newton per kilo-Newton (N/kN). Older texts still use the wrong unit of kilogram-force per tonne (kgf/t).
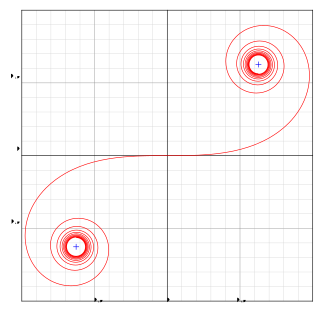
An Euler spiral is a curve whose curvature changes linearly with its curve length. The curve is also referred to as clothoids or Cornu spirals. The behavior of Fresnel integrals can be illustrated by Euler spirals, a connection first made by Alfred Marie Cornu 1874. Euler's spiral is a type of superspiral that has the property of a monotonic curvature function.

The minimum railway curve radius is the shortest allowable design radius for the centerline of railway tracks under a particular set of conditions. It has an important bearing on construction costs and operating costs and, in combination with superelevation in the case of train tracks, determines the maximum safe speed of a curve. The minimum radius of a curve is one parameter in the design of railway vehicles as well as trams; monorails and automated guideways are also subject to a minimum radius.

In Newtonian mechanics, the centrifugal force is an inertial force that appears to act on all objects when viewed in a rotating frame of reference. It is directed radially away from the axis of rotation. The magnitude of centrifugal force F on an object of mass m at the distance r from the axis of rotation of a frame of reference rotating with angular velocity ω is:

Rail speed limits in the United States are regulated by the Federal Railroad Administration. Railroads also implement their own limits and enforce speed limits. Speed restrictions are based on a number of factors including curvature, signaling, track condition, and the presence of grade crossings. Like road speed limits in the United States, speed limits for tracks and trains are measured in miles per hour (mph).

The geometric design of roads is the branch of highway engineering concerned with the positioning of the physical elements of the roadway according to standards and constraints. The basic objectives in geometric design are to optimize efficiency and safety while minimizing cost and environmental damage. Geometric design also affects an emerging fifth objective called "livability," which is defined as designing roads to foster broader community goals, including providing access to employment, schools, businesses and residences, accommodate a range of travel modes such as walking, bicycling, transit, and automobiles, and minimizing fuel use, emissions and environmental damage.
Contact mechanics is the study of the deformation of solids that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and frictional forces in the tangential direction. Frictional contact mechanics is the study of the deformation of bodies in the presence of frictional effects, whereas frictionless contact mechanics assumes the absence of such effects.

Track geometry is concerned with the properties and relations of points, lines, curves, and surfaces in the three-dimensional positioning of railroad track. The term is also applied to measurements used in design, construction and maintenance of track. Track geometry involves standards, speed limits and other regulations in the areas of track gauge, alignment, elevation, curvature and track surface. Standards are usually separately expressed for horizontal and vertical layouts although track geometry is three-dimensional.

The cant of a railway track or camber of a road is the rate of change in elevation (height) between the two rails or edges of the road. This is normally greater where the railway or road is curved; raising the outer rail or the outer edge of the road creates a banked turn, thus allowing vehicles to travel round the curve at greater speeds than would be possible if the surface were level.






















