
In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on biologically inspired operators such as mutation, crossover and selection. Some examples of GA applications include optimizing decision trees for better performance, solving sudoku puzzles, hyperparameter optimization, causal inference, etc.

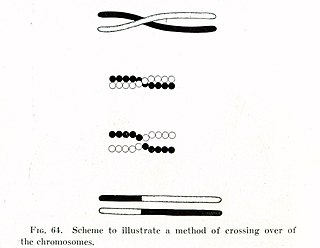
Chromosomal crossover, or crossing over, is the exchange of genetic material during sexual reproduction between two homologous chromosomes' non-sister chromatids that results in recombinant chromosomes. It is one of the final phases of genetic recombination, which occurs in the pachytene stage of prophase I of meiosis during a process called synapsis. Synapsis begins before the synaptonemal complex develops and is not completed until near the end of prophase I. Crossover usually occurs when matching regions on matching chromosomes break and then reconnect to the other chromosome.

Genetic recombination is the exchange of genetic material between different organisms which leads to production of offspring with combinations of traits that differ from those found in either parent. In eukaryotes, genetic recombination during meiosis can lead to a novel set of genetic information that can be further passed on from parents to offspring. Most recombination occurs naturally and can be classified into two types: (1) interchromosomal recombination, occurring through independent assortment of alleles whose loci are on different but homologous chromosomes ; & (2) intrachromosomal recombination, occurring through crossing over.
In computational intelligence (CI), an evolutionary algorithm (EA) is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions. Evolution of the population then takes place after the repeated application of the above operators.

In computer science, evolutionary computation is a family of algorithms for global optimization inspired by biological evolution, and the subfield of artificial intelligence and soft computing studying these algorithms. In technical terms, they are a family of population-based trial and error problem solvers with a metaheuristic or stochastic optimization character.
Genetic linkage is the tendency of DNA sequences that are close together on a chromosome to be inherited together during the meiosis phase of sexual reproduction. Two genetic markers that are physically near to each other are unlikely to be separated onto different chromatids during chromosomal crossover, and are therefore said to be more linked than markers that are far apart. In other words, the nearer two genes are on a chromosome, the lower the chance of recombination between them, and the more likely they are to be inherited together. Markers on different chromosomes are perfectly unlinked, although the penetrance of potentially deleterious alleles may be influenced by the presence of other alleles, and these other alleles may be located on other chromosomes than that on which a particular potentially deleterious allele is located.
In evolutionary genetics, Muller's ratchet is a process which, in the absence of recombination, results in an accumulation of irreversible deleterious mutations. This happens because in the absence of recombination, and assuming reverse mutations are rare, offspring bear at least as much mutational load as their parents. Muller proposed this mechanism as one reason why sexual reproduction may be favored over asexual reproduction, as sexual organisms benefit from recombination and consequent elimination of deleterious mutations. The negative effect of accumulating irreversible deleterious mutations may not be prevalent in organisms which, while they reproduce asexually, also undergo other forms of recombination. This effect has also been observed in those regions of the genomes of sexual organisms that do not undergo recombination.

Genetic variation is the difference in DNA among individuals or the differences between populations among the same species. The multiple sources of genetic variation include mutation and genetic recombination. Mutations are the ultimate sources of genetic variation, but other mechanisms, such as genetic drift, contribute to it, as well.
A genetic operator is an operator used in genetic algorithms to guide the algorithm towards a solution to a given problem. There are three main types of operators, which must work in conjunction with one another in order for the algorithm to be successful. Genetic operators are used to create and maintain genetic diversity, combine existing solutions into new solutions (crossover) and select between solutions (selection). In his book discussing the use of genetic programming for the optimization of complex problems, computer scientist John Koza has also identified an 'inversion' or 'permutation' operator; however, the effectiveness of this operator has never been conclusively demonstrated and this operator is rarely discussed.
A fitness function is a particular type of objective function that is used to summarise, as a single figure of merit, how close a given design solution is to achieving the set aims. Fitness functions are used in software architecture and evolutionary algorithms (EA), such as genetic programming and genetic algorithms to guide simulations towards optimal design solutions.
Mutation is a genetic operator used to maintain genetic diversity of the chromosomes of a population of a genetic or, more generally, an evolutionary algorithm (EA). It is analogous to biological mutation.
In genetic algorithms (GA), or more general, evolutionary algorithms (EA), a chromosome is a set of parameters which define a proposed solution of the problem that the evolutionary algorithm is trying to solve. The set of all solutions, also called individuals according to the biological model, is known as the population. The genome of an individual consists of one, more rarely of several, chromosomes and corresponds to the genetic representation of the task to be solved. A chromosome is composed of a set of genes, where a gene consists of one or more semantically connected parameters, which are often also called decision variables. They determine one or more phenotypic characteristics of the individual or at least have an influence on them. In the basic form of genetic algorithms, the chromosome is represented as a binary string, while in later variants and in EAs in general, a wide variety of other data structures are used.
A haplotype is a group of alleles in an organism that are inherited together from a single parent.

Evolution of sexual reproduction describes how sexually reproducing animals, plants, fungi and protists could have evolved from a common ancestor that was a single-celled eukaryotic species. Sexual reproduction is widespread in eukaryotes, though a few eukaryotic species have secondarily lost the ability to reproduce sexually, such as Bdelloidea, and some plants and animals routinely reproduce asexually without entirely having lost sex. The evolution of sexual reproduction contains two related yet distinct themes: its origin and its maintenance. Bacteria and Archaea (prokaryotes) have processes that can transfer DNA from one cell to another, but it is unclear if these processes are evolutionarily related to sexual reproduction in Eukaryotes. In eukaryotes, true sexual reproduction by meiosis and cell fusion is thought to have arisen in the last eukaryotic common ancestor, possibly via several processes of varying success, and then to have persisted.
In computer science, an evolution strategy (ES) is an optimization technique based on ideas of evolution. It belongs to the general class of evolutionary computation or artificial evolution methodologies.
In computer programming, gene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype–phenotype system, benefiting from a simple genome to keep and transmit the genetic information and a complex phenotype to explore the environment and adapt to it.
Selection is the stage of a genetic algorithm or more general evolutionary algorithm in which individual genomes are chosen from a population for later breeding. Selection mechanisms are also used to choose candidate solutions (individuals) for the next generation. Retaining the best individuals in a generation unchanged in the next generation, is called elitism or elitist selection. It is a successful (slight) variant of the general process of constructing a new population.
In evolutionary algorithms (EA), the term of premature convergence means that a population for an optimization problem converged too early, resulting in being suboptimal. In this context, the parental solutions, through the aid of genetic operators, are not able to generate offspring that are superior to, or outperform, their parents. Premature convergence is a common problem found in evolutionary algorithms in general and genetic algorithms in particular, as it leads to a loss, or convergence of, a large number of alleles, subsequently making it very difficult to search for a specific gene in which the alleles were present. An allele is considered lost if, in a population, a gene is present, where all individuals are sharing the same value for that particular gene. An allele is, as defined by De Jong, considered to be a converged allele, when 95% of a population share the same value for a certain gene.
In computer programming, genetic representation is a way of presenting solutions/individuals in evolutionary computation methods. The term encompasses both the concrete data structures and data types used to realize the genetic material of the candidate solutions in the form of a genome, and the relationships between search space and problem space. In the simplest case, the search space corresponds to the problem space. The choice of problem representation is tied to the choice of genetic operators, both of which have a decisive effect on the efficiency of the optimization. Genetic representation can encode appearance, behavior, physical qualities of individuals. Difference in genetic representations is one of the major criteria drawing a line between known classes of evolutionary computation.
A memetic algorithm (MA) in computer science and operations research, is an extension of the traditional genetic algorithm (GA) or more general evolutionary algorithm (EA). It may provide a sufficiently good solution to an optimization problem. It uses a suitable heuristic or local search technique to improve the quality of solutions generated by the EA and to reduce the likelihood of premature convergence.

























































