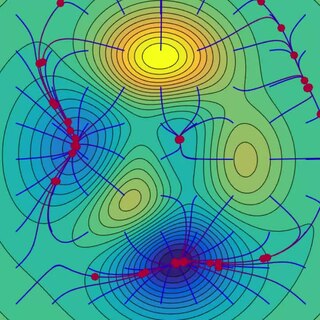
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for finding a local minimum of a differentiable multivariate function
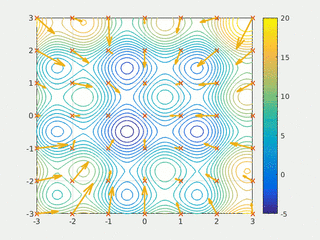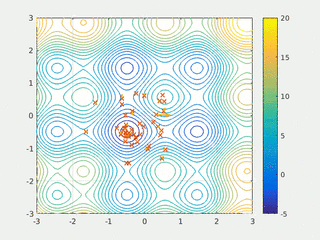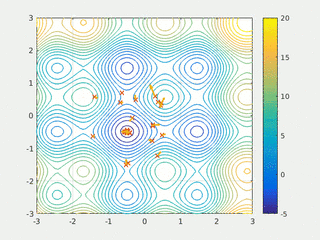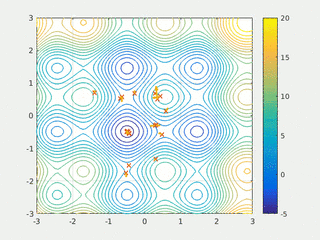
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. Sometimes loosely referred to as "the" exponential family, this class of distributions is distinct because they all possess a variety of desirable properties, most importantly the existence of a sufficient statistic.
A directional derivative is a concept in multivariable calculus that measures the rate at which a function changes in a particular direction at a given point.
Feature selection is the process of selecting a subset of relevant features for use in model construction. Stylometry and DNA microarray analysis are two cases where feature selection is used. It should be distinguished from feature extraction.

In directional statistics, the Kent distribution, also known as the 5-parameter Fisher–Bingham distribution, is a probability distribution on the unit sphere. It is the analogue on S2 of the bivariate normal distribution with an unconstrained covariance matrix. The Kent distribution was proposed by John T. Kent in 1982, and is used in geology as well as bioinformatics.
In directional statistics, the von Mises–Fisher distribution, is a probability distribution on the -sphere in . If the distribution reduces to the von Mises distribution on the circle.
The cross-entropy (CE) method is a Monte Carlo method for importance sampling and optimization. It is applicable to both combinatorial and continuous problems, with either a static or noisy objective.

In probability theory and statistics, the normal-inverse-gamma distribution is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.
In continuum mechanics, the most commonly used measure of stress is the Cauchy stress tensor, often called simply the stress tensor or "true stress". However, several alternative measures of stress can be defined:
- The Kirchhoff stress.
- The nominal stress.
- The Piola–Kirchhoff stress tensors
- The first Piola–Kirchhoff stress. This stress tensor is the transpose of the nominal stress.
- The second Piola–Kirchhoff stress or PK2 stress.
- The Biot stress

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: The line integral of a vector field over a loop is equal to its curl through the enclosed surface. It is illustrated in the figure, where the direction of positive circulation of the bounding contour ∂Σ, and the direction n of positive flux through the surface Σ, are related by a right-hand-rule. For the right hand the fingers circulate along ∂Σ and the thumb is directed along n.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.
In operations research, cuckoo search is an optimization algorithm developed by Xin-She Yang and Suash Deb in 2009. It has been shown to be a special case of the well-known -evolution strategy. It was inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of host birds of other species. Some host birds can engage direct conflict with the intruding cuckoos. For example, if a host bird discovers the eggs are not their own, it will either throw these alien eggs away or simply abandon its nest and build a new nest elsewhere. Some cuckoo species such as the New World brood-parasitic Tapera have evolved in such a way that female parasitic cuckoos are often very specialized in the mimicry in colors and pattern of the eggs of a few chosen host species. Cuckoo search idealized such breeding behavior, and thus can be applied for various optimization problems.
The Bat algorithm is a metaheuristic algorithm for global optimization. It was inspired by the echolocation behaviour of microbats, with varying pulse rates of emission and loudness. The Bat algorithm was developed by Xin-She Yang in 2010.
In computer science, imperialist competitive algorithms are a type of computational method used to solve optimization problems of different types. Like most of the methods in the area of evolutionary computation, ICA does not need the gradient of the function in its optimization process. From a specific point of view, ICA can be thought of as the social counterpart of genetic algorithms (GAs). ICA is the mathematical model and the computer simulation of human social evolution, while GAs are based on the biological evolution of species.
In statistics, the matrix t-distribution is the generalization of the multivariate t-distribution from vectors to matrices. The matrix t-distribution shares the same relationship with the multivariate t-distribution that the matrix normal distribution shares with the multivariate normal distribution. For example, the matrix t-distribution is the compound distribution that results from sampling from a matrix normal distribution having sampled the covariance matrix of the matrix normal from an inverse Wishart distribution.
In statistics and physics, multicanonical ensemble is a Markov chain Monte Carlo sampling technique that uses the Metropolis–Hastings algorithm to compute integrals where the integrand has a rough landscape with multiple local minima. It samples states according to the inverse of the density of states, which has to be known a priori or be computed using other techniques like the Wang and Landau algorithm. Multicanonical sampling is an important technique for spin systems like the Ising model or spin glasses.

Dispersive flies optimisation (DFO) is a bare-bones swarm intelligence algorithm which is inspired by the swarming behaviour of flies hovering over food sources. DFO is a simple optimiser which works by iteratively trying to improve a candidate solution with regard to a numerical measure that is calculated by a fitness function. Each member of the population, a fly or an agent, holds a candidate solution whose suitability can be evaluated by their fitness value. Optimisation problems are often formulated as either minimisation or maximisation problems.

The hyperbolastic functions, also known as hyperbolastic growth models, are mathematical functions that are used in medical statistical modeling. These models were originally developed to capture the growth dynamics of multicellular tumor spheres, and were introduced in 2005 by Mohammad Tabatabai, David Williams, and Zoran Bursac. The precision of hyperbolastic functions in modeling real world problems is somewhat due to their flexibility in their point of inflection. These functions can be used in a wide variety of modeling problems such as tumor growth, stem cell proliferation, pharma kinetics, cancer growth, sigmoid activation function in neural networks, and epidemiological disease progression or regression.























