
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.

Meantone temperaments are musical temperaments, that is a variety of tuning systems, obtained by narrowing the fifths so that their ratio is slightly less than 3:2, in order to push the thirds closer to pure. Meantone temperaments are constructed the same way as Pythagorean tuning, as a stack of equal fifths, but it is a temperament in that the fifths are not pure.

In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125). Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the Pythagorean major third to a just major third.

In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals produced by other tuning systems, including Pythagorean and most meantone temperaments.
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B♯, or D♭ and C♯. It is equal to the frequency ratio (1.5)12⁄27 = 531441⁄524288 ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often "temper" is the Pythagorean comma.

In classical music from Western culture, a diesis is either an accidental, or a very small musical interval, usually defined as the difference between an octave and three justly tuned major thirds, equal to 128:125 or about 41.06 cents. In 12-tone equal temperament three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B♯. The difference between C-C' (2:1) and C-B♯ (125:64) is the diesis (128:125). Notice that this coincides with the interval between B♯ and C', also called a diminished second.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

In music, the schisma (also spelled skhisma) is the interval between a Pythagorean comma (531441:524288) and a syntonic comma (81:80) and equals 5(38)⁄215 or 32805:32768 = 1.00113, which is 1.9537 cents. It may also be defined as:

In music, a ditone is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
Quarter-comma meantone, or 1⁄4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81 : 80), with respect to its just intonation used in Pythagorean tuning ; the result is 3/2 × 1⁄4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.

In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET or 31-EDO, also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps. Each step represents a frequency ratio of 31√2, or 38.71 cents.

In musical tuning theory, a Pythagorean interval is a musical interval with a frequency ratio equal to a power of two divided by a power of three, or vice versa. For instance, the perfect fifth with ratio 3/2 (equivalent to 31/ 21) and the perfect fourth with ratio 4/3 (equivalent to 22/ 31) are Pythagorean intervals.

In musical tuning, a temperament is a tuning system that slightly compromises the pure intervals of just intonation to meet other requirements. Most modern Western musical instruments are tuned in the equal temperament system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve fifth intervals in the circle of fifths so that they accommodate pure octaves and produce certain sizes of major thirds is called a temperament." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various keys, and lack any way to alter pitch of a note in performance. Historically, the use of just intonation, Pythagorean tuning and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance in other keys.
In musical theory, 34 equal temperament, also referred to as 34-TET, 34-EDO or 34-ET, is the tempered tuning derived by dividing the octave into 34 equal-sized steps. Each step represents a frequency ratio of 34√2, or 35.29 cents.
In music, 41 equal temperament, abbreviated 41-TET, 41-EDO, or 41-ET, is the tempered scale derived by dividing the octave into 41 equally sized steps. Each step represents a frequency ratio of 21/41, or 29.27 cents, an interval close in size to the septimal comma. 41-ET can be seen as a tuning of the schismatic, magic and miracle temperaments. It is the second smallest equal temperament, after 29-ET, whose perfect fifth is closer to just intonation than that of 12-ET. In other words, is a better approximation to the ratio than either or .
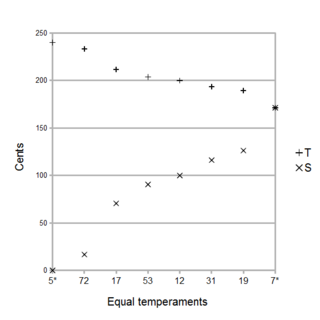
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.
















