
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.
In music, two written notes have enharmonic equivalence if they produce the same pitch but are notated differently. Similarly, written intervals, chords, or key signatures are considered enharmonic if they represent identical pitches that are notated differently. The term derives from Latin enharmonicus, in turn from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος, from ἐν ('in') and ἁρμονία ('harmony').

In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals produced by other tuning systems, including Pythagorean and most meantone temperaments.
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B♯, or D♭ and C♯. It is equal to the frequency ratio (1.5)12⁄27 = 531441⁄524288 ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often "temper" is the Pythagorean comma.

In classical music from Western culture, a diesis ( DY-ə-siss or enharmonic diesis, plural dieses, or "difference"; Greek: δίεσις "leak" or "escape" is either an accidental, or a very small musical interval, usually defined as the difference between an octave and three justly tuned major thirds, equal to 128:125 or about 41.06 cents. In 12-tone equal temperament three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave spans from C to C′, and three justly tuned major thirds span from C to B♯. The difference between C-C′ and C-B♯ is the diesis. Notice that this coincides with the interval between B♯ and C', also called a diminished second.

In music theory, the circle of fifths is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music, the sequence is: C, G, D, A, E, B, F♯, C♯, G♯, D♯, A♯, E♯ (F), C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.

A semitone, also called a minor second, half step, or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale, visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C♯; the interval between them is a semitone.

In music, an augmented sixth is an interval produced by widening a major sixth by a chromatic semitone. For instance, the interval from C to A is a major sixth, nine semitones wide, and both the intervals from C♭ to A, and from C to A♯ are augmented sixths, spanning ten semitones. Being augmented, it is considered a dissonant interval.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.

In classical music from Western culture, an augmented second is an interval that, in 12-tone equal temperament, is sonically equivalent to a minor third, spanning three semitones, and is created by widening a major second by a chromatic semitone. For instance, the interval from C to D is a major second, two semitones wide, and the interval from C to D♯ is an augmented second, spanning three semitones.
Quarter-comma meantone, or 1 / 4 -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma ( 81 : 80 ), with respect to its just intonation used in Pythagorean tuning ; the result is 3 / 2 × [ 80 / 81 ] 1 / 4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.

In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET or 31-EDO, also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps. Each step represents a frequency ratio of 31√2, or 38.71 cents.

In classical music from Western culture, a diminished third is the musical interval produced by narrowing a minor third by a chromatic semitone. For instance, the interval from A to C is a minor third, three semitones wide, and both the intervals from A♯ to C, and from A to C♭ are diminished thirds, two semitones wide. Being diminished, it is considered a dissonant interval.

Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.
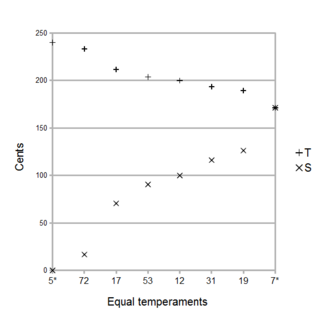
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

In classical music from Western culture, an augmented seventh is an interval produced by widening a major seventh by a chromatic semitone. For instance, the interval from C to B is a major seventh, eleven semitones wide, and both the intervals from C♭ to B, and from C to B♯ are augmented sevenths, spanning twelve semitones. Being augmented, it is classified as a dissonant interval. However, it is enharmonically equivalent to the perfect octave.

In classical music from Western culture, a diminished sixth is an interval produced by narrowing a minor sixth by a chromatic semitone. For example, the interval from A to F is a minor sixth, eight semitones wide, and both the intervals from A♯ to F, and from A to F♭ are diminished sixths, spanning seven semitones. Being diminished, it is considered a dissonant interval, despite being equivalent to an interval known for its consonance.


















