Septimal third tone

Last updated February 21, 2019

A septimal 1/3-tone (in music) is an interval with the ratio of 28:27,^[1] which is the difference between the perfect fourth and the supermajor third. It is about 62.96 cents wide. The septimal 1/3-tone can be viewed either as a musical interval in its own right, or as a comma; if it is tempered out in a given tuning system, the distinction between these two intervals is lost. The septimal 1/3-tone may be derived from the harmonic series as the interval between the twenty-seventh and twenty-eighth harmonics. It may be considered a diesis.^[2]

Music is an art form and cultural activity whose medium is sound organized in time. General definitions of music include common elements such as pitch, rhythm, dynamics, and the sonic qualities of timbre and texture. Different styles or types of music may emphasize, de-emphasize or omit some of these elements. Music is performed with a vast range of instruments and vocal techniques ranging from singing to rapping; there are solely instrumental pieces, solely vocal pieces and pieces that combine singing and instruments. The word derives from Greek μουσική . See glossary of musical terminology.

In music theory, an interval is the difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth is the fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F is the fifth semitone above C, and there are four staff positions between C and F. Diminished and augmented fourths span the same number of staff positions, but consist of a different number of semitones.

The septimal 1/3-tone, along with the septimal diesis is tempered out by five-tone equal temperament, and equal temperaments which divide the octave into a small multiple of 5 steps, such as 15-TET and 25-TET. This family of scales is known as Blackwood temperament in honor of Easley Blackwood, Jr., who first analyzed 10-note subsets of 15-TET that take advantage of the temperament.

In music, septimal diesis is an interval with the ratio of 49:48 play (help·info), which is the difference between the septimal whole tone and the septimal minor third. It is about 35.7 cents wide, which is narrower than a quarter-tone but wider than the septimal comma. It may also be the ratio 36:35, or 48.77 cents. Play (help·info)

In music, 15 equal temperament, called 15-TET, 15-EDO, or 15-ET, is a tempered scale derived by dividing the octave into 15 equal steps. Each step represents a frequency ratio of ¹⁵√2, or 80 cents. Because 15 factors into 3 times 5, it can be seen as being made up of three scales of 5 equal divisions of the octave, each of which resembles the Slendro scale in Indonesian gamelan. 15 equal temperament is not a meantone system.

When added to the 15:14 semitone, the 21:20 semitone and 28:27 semitone produce the 9:8 tone (major tone) and 10:9 tone (minor tone), respectively.

In music, a septimal diatonic semitone is the interval 15:14 Play (help·info). It is about 119.44 cents. The septimal diatonic semitone may be derived from the harmonic series as the interval between the fourteenth and fifteenth harmonics.

In music, a septimal chromatic semitone or minor semitone is the interval 21:20. It is about 84.47 cents. The septimal chromatic semitone may be derived from the harmonic series as the interval between the twentieth and twenty-first harmonics.

It is the difference between 7/6 and 9/8 (tritē and paramesē).^[3]^[4]

Septimal sixth tone

The septimal sixth tone, also called the jubilisma, is a 7-limit musical interval approximately the size of 1/6 of a whole tone (203.91/6=33.99 cents). An interval with the ratio of 50:49 ( play (help·info)), about 34.98 cents, which in just intonation is the difference between the lesser septimal (7:5) tritone, and its inversion, the greater septimal tritone (10:7). This interval is tempered out by 12-TET and 22-TET, but not by 19-TET, 31-TET or any other odd division of the octave.

In music, septimal meantone temperament, also called standard septimal meantone or simply septimal meantone, refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Meantone temperament represents a frequency ratio of approximately 5 by means of four fifths, so that the major third, for instance C-E, is obtained from two tones in succession. Septimal meantone represents the frequency ratio of 56 (7*2³) by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C-A♯, not C-B♭, represents a 7:4 interval in septimal meantone.

In music, just intonation or pure intonation is the tuning of musical intervals as (small) whole number ratios of frequencies. Any interval tuned in this way is called a just interval. Just intervals and chords are aggregates of harmonic series partials and may be seen as sharing a (lower) implied fundamental. For example, a tone with a frequency of 300 Hz and another with a frequency of 200 Hz are both multiples of 100 Hz. Their interval is, therefore, an aggregate of the second and third partials of the harmonic series of an implied fundamental frequency 100 Hz.

In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B. According to this definition, within a diatonic scale there is only one tritone for each octave. For instance, the above-mentioned interval F–B is the only tritone formed from the notes of the C major scale. A tritone is also commonly defined as an interval spanning six semitones. According to this definition, a diatonic scale contains two tritones for each octave. For instance, the above-mentioned C major scale contains the tritones F–B and B–F. In twelve-equal temperament, the tritone divides the octave exactly in half.

Related Research Articles

An equal temperament is a musical temperament, or a system of tuning, in which the frequency interval between every pair of adjacent notes has the same ratio. In other words, the ratios of the frequencies of any adjacent pair of notes is the same, and, as pitch is perceived roughly as the logarithm of frequency, equal perceived "distance" from every note to its nearest neighbor.

In classical music from Western culture, a diesis is either an accidental, or a very small musical interval, usually defined as the difference between an octave and three justly tuned major thirds, equal to 128:125 or about 41.06 cents. In 12-tone equal temperament three major thirds in a row equal an octave, but three justly-tuned major thirds fall quite a bit narrow of an octave, and the diesis describes the amount by which they are short. For instance, an octave (2:1) spans from C to C', and three justly tuned major thirds (5:4) span from C to B♯. The difference between C-C' (2:1) and C-B♯ (125:64) is the diesis (128:125). Notice that this coincides with the interval between B♯ and C', also called a diminished second.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide as a semitone, which itself is half a whole tone.

In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81/80 are considered the same note because the 12 note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.

In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET, 31-EDO, also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps. Play (help·info) Each step represents a frequency ratio of ³¹√2, or 38.71 cents.

In music, the ratio 225/224 is called the septimal kleisma (play (help·info)). It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2⁻⁵ 3² 5² 7⁻¹, which can be rewritten 2⁻¹ (5/4)² (9/7). That says that it is the amount that two major thirds of 5/4 and a septimal major third, or supermajor third, of 9/7 exceeds the octave. If the septimal kleisma is tempered out, as it is for instance in miracle temperament, septimal meantone temperament, septimal magic temperament and in many equal temperaments, for example 12, 19, 22, 31, 41, 53, 72 or 84 equal, then an augmented triad consisting of two major thirds and a supermajor third making up an octave becomes possible. The existence of such a chord, which might be termed the septimal kleisma augmented triad, is a significant feature of a tuning system.

In music, 19 equal temperament, called 19 TET, 19 EDO, or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps. Each step represents a frequency ratio of ¹⁹√2, or 63.16 cents.

A septimal comma is a small musical interval in just intonation that contains the number seven in its prime factorization. There is more than one such interval, so the term septimal comma is ambiguous, but it most commonly refers to the interval 64/63. Play (help·info)

In music, the septimal minor thirdplay (help·info), also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5. In 24-tone equal temperament five quarter tones approximate the septimal minor third at 250 cents.

In musical theory, 34 equal temperament, also referred to as 34-tet, 34-edo or 34-et, is the tempered tuning derived by dividing the octave into 34 equal-sized steps. Play (help·info) Each step represents a frequency ratio of ³⁴√2, or 35.29 cents Play (help·info).

A septimal quarter tone is an interval with the ratio of 36:35, which is the difference between the septimal minor third and the Just minor third, or about 48.77 cents wide. The name derives from the interval being the 7-limit approximation of a quarter tone. The septimal quarter tone can be viewed either as a musical interval in its own right, or as a comma; if it is tempered out in a given tuning system, the distinction between the two different types of minor thirds is lost. The septimal quarter tone may be derived from the harmonic series as the interval between the thirty-fifth and thirty-sixth harmonics.

In music, 41 equal temperament, abbreviated 41-tET, 41-EDO, or 41-ET, is the tempered scale derived by dividing the octave into 41 equally sized steps. Play (help·info) Each step represents a frequency ratio of 2^1/41, or 29.27 cents, an interval close in size to the septimal comma. 41-ET can be seen as a tuning of the schismatic, magic and miracle temperaments. It is the second smallest equal temperament, after 29-ET, whose perfect fifth is closer to just intonation than that of 12-ET. In other words, $is a better approximation to the ratio than either or .$

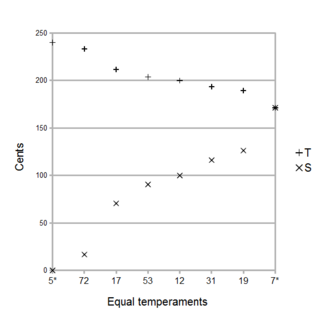
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

A septimal tritone is a tritone that involves the factor seven. There are two that are inverses. The lesser septimal tritone is the musical interval with ratio 7:5. The greater septimal tritone, is an interval with ratio 10:7. They are also known as the sub-fifth and super-fourth, or subminor fifth and supermajor fourth, respectively.

In music theory, a neutral interval is an interval that is neither a major nor minor, but instead in between. For example, in equal temperament, a major third is 400 cents, a minor third is 300 cents, and a neutral third is 350 cents. A neutral interval inverts to a neutral interval. For example, the inverse of a neutral third is a neutral sixth.

References

↑ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiv. ISBN 0-8247-4714-3. 1/3-tone, Archytas inferior 1/4-tone.
↑ Thomas Christensen, ed. (2002). The Cambridge History of Western Music Theory, p.186. ISBN 9780521623711.
↑ Huffman, Carl (2005). Archytas of Tarentum: Pythagorean, Philosopher and Mathematician King, p.420. ISBN 9781139444071.
↑ Andrew Barker, ed. (2004). Greek Musical Writings: Volume 2, Harmonic and Acoustic Theory, p.51. ISBN 9780521616973.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiv. ISBN 0-8247-4714-3. 1/3-tone, Archytas inferior 1/4-tone.

[2] Thomas Christensen, ed. (2002). The Cambridge History of Western Music Theory, p.186. ISBN 9780521623711.

[3] Huffman, Carl (2005). Archytas of Tarentum: Pythagorean, Philosopher and Mathematician King, p.420. ISBN 9781139444071.

[4] Andrew Barker, ed. (2004). Greek Musical Writings: Volume 2, Harmonic and Acoustic Theory, p.51. ISBN 9780521616973.