
In mathematics, a complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a symbol called the imaginary unit, and satisfying the equation i2 = −1. Because no "real" number satisfies this equation, i was called an imaginary number by René Descartes. For the complex number a + bi, a is called the real part and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form a + bε, where a and b are real numbers, and ε is a symbol taken to satisfy .
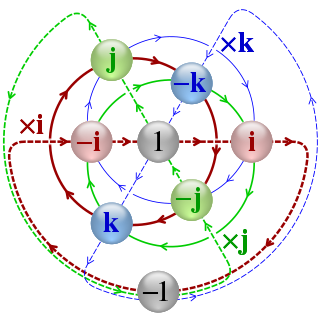
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.
In mathematics, de Moivre's formula states that for any real number x and integer n it holds that

In group theory, the quaternion group Q8 (sometimes just denoted by Q) is a non-abelian group of order eight, isomorphic to the eight-element subset of the quaternions under multiplication. It is given by the group presentation
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance, and orientation. Every non-trivial rotation is determined by its axis of rotation and its angle of rotation. Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map satisfies the definition of a rotation. Owing to the above properties, the set of all rotations is a group under composition. Rotations are not commutative, making it a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable; so it is in fact a Lie group. It is compact and has dimension 3.

In mathematics, the special unitary group of degree n, denoted SU(n), is the Lie group of n × n unitary matrices with determinant 1.

Eduard Study, more properly Christian Hugo Eduard Study, was a German mathematician known for work on invariant theory of ternary forms (1889) and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or a vector of small quantities. The infinitesimal conditions are the result of applying the approach of differential calculus to solving a problem with constraints. The name is an analogy to non-rigid structures that deform slightly to accommodate external forces.
In abstract algebra, the biquaternions are the numbers w + xi + yj + zk, where w, x, y, and z are complex numbers, or variants thereof, and the elements of {1, i, j, k} multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.
In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products, but for general Banach spaces or locally convex topological vector spaces the theory is notoriously subtle.
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold. Then the Dolbeault cohomology groups depend on a pair of integers p and q and are realized as a subquotient of the space of complex differential forms of degree (p,q).
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by Hermann Weyl. There is a closely related formula for the character of an irreducible representation of a semisimple Lie algebra. In Weyl's approach to the representation theory of connected compact Lie groups, the proof of the character formula is a key step in proving that every dominant integral element actually arises as the highest weight of some irreducible representation. Important consequences of the character formula are the Weyl dimension formula and the Kostant multiplicity formula.

In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form A + εB, where A and B are ordinary quaternions and ε is the dual unit, which satisfies ε2 = 0 and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra.
In mathematics, specifically the theory of quadratic forms, an ε-quadratic form is a generalization of quadratic forms to skew-symmetric settings and to *-rings; ε = ±1, accordingly for symmetric or skew-symmetric. They are also called -quadratic forms, particularly in the context of surgery theory.
In mathematics, quaternionic analysis is the study of functions with quaternions as the domain and/or range. Such functions can be called functions of a quaternion variable just as functions of a real variable or a complex variable are called.
In representation theory of mathematics, the Waldspurger formula relates the special values of two L-functions of two related admissible irreducible representations. Let k be the base field, f be an automorphic form over k, π be the representation associated via the Jacquet–Langlands correspondence with f. Goro Shimura (1976) proved this formula, when and f is a cusp form; Günter Harder made the same discovery at the same time in an unpublished paper. Marie-France Vignéras (1980) proved this formula, when { and f is a newform. Jean-Loup Waldspurger, for whom the formula is named, reproved and generalized the result of Vignéras in 1985 via a totally different method which was widely used thereafter by mathematicians to prove similar formulas.
The Laguerre transformations or axial homographies are an analogue of Möbius transformations over the dual numbers. When studying these transformations, the dual numbers are often interpreted as representing oriented lines on the plane. The Laguerre transformations map lines to lines, and include in particular all isometries of the plane.






























































