Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. Maxwell's equations describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. One important consequence of the equations is that they demonstrate how fluctuating electric and magnetic fields propagate at the speed of light. Known as electromagnetic radiation, these waves may occur at various wavelengths to produce a spectrum from radio waves to γ-rays. The equations are named after the physicist and mathematician James Clerk Maxwell, who between 1861 and 1862 published an early form of the equations that included the Lorentz force law. He also first used the equations to propose that light is an electromagnetic phenomenon.

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.

A capillary wave is a wave traveling along the phase boundary of a fluid, whose dynamics and phase velocity are dominated by the effects of surface tension.

The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density and pressure . The equations for negative spatial curvature were given by Friedmann in 1924.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.

In physics, Larmor precession is the precession of the magnetic moment of an object about an external magnetic field. Objects with a magnetic moment also have angular momentum and effective internal electric current proportional to their angular momentum; these include electrons, protons, other fermions, many atomic and nuclear systems, as well as classical macroscopic systems. The external magnetic field exerts a torque on the magnetic moment,
The magnetic Reynolds number (Rm) is the magnetic analogue of the Reynolds number, a fundamental dimensionless group that occurs in magnetohydrodynamics. It gives an estimate of the relative effects of advection or induction of a magnetic field by the motion of a conducting medium, often a fluid, to magnetic diffusion. It is typically defined by:
In mathematics, a π-system on a set Ω is a collection P of certain subsets of Ω, such that

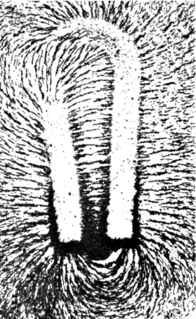
A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the field is perpendicular to the normal vector, . Both the cross-sectional area of the tube and the field contained may vary along the length of the tube, but the magnetic flux is always constant.
In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor which incorporates the energy–momentum of gravity. It allows the energy–momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy–momentum to form a conserved current within the framework of general relativity, so that the total energy–momentum crossing the hypersurface of any compact space–time hypervolume vanishes.
The Chandrasekhar number is a dimensionless quantity used in magnetic convection to represent ratio of the Lorentz force to the viscosity. It is named after the Indian astrophysicist Subrahmanyan Chandrasekhar.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:
In fluid dynamics, a flow with periodic variations is known as pulsatile flow, or as Womersley flow. The flow profiles was first derived by John R. Womersley (1907–1958) in his work with blood flow in arteries. The cardiovascular system of chordate animals is a very good example where pulsatile flow is found, but pulsatile flow is also observed in engines and hydraulic systems, as a result of rotating mechanisms pumping the fluid.
The Stuart number (N), also known as magnetic interaction parameter, is a dimensionless number of fluids, i.e. gases or liquids.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.
How the plasma transport is reduced by the strength of the external magnetic field is of great concern in studying magnetic confinement of fusion plasma. The plasma diffusion may be classified by the classical diffusion of B−2 scaling, the Bohm diffusion conjectured to follow the B−1 scaling, and the Hsu diffusion of B−3/2 scaling. Here, B is the external magnetic field.
A model of a charged membrane introduced by Paul Dirac in 1962. Dirac's original motivation was to explain the mass of the muon as an excitation of the ground state corresponding to an electron. Anticipating the birth of string theory by almost a decade, he was the first to introduce what is now called a type of Nambu–Goto action for membranes.