The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.
In finance, a put or put option is a financial market derivative instrument which gives the holder the right to sell an asset, at a specified price, by a specified date to the writer of the put. The purchase of a put option is interpreted as a negative sentiment about the future value of the underlying stock. The term "put" comes from the fact that the owner has the right to "put up for sale" the stock or index.
In financial mathematics, put–call parity defines a relationship between the price of a European call option and European put option, both with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to a single forward contract at this strike price and expiry. This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract.
In finance, a straddle strategy refers to two transactions that share the same security, with positions that offset one another. One holds long risk, the other short. As a result, it involves the purchase or sale of particular option derivatives that allow the holder to profit based on how much the price of the underlying security moves, regardless of the direction of price movement.

In finance, the strike price of an option is a fixed price at which the owner of the option can buy, or sell, the underlying security or commodity. The strike price may be set by reference to the spot price, which is the market price of the underlying security or commodity on the day an option is taken out. Alternatively, the strike price may be fixed at a discount or premium.
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
In finance, moneyness is the relative position of the current price of an underlying asset with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification: if the derivative would have positive intrinsic value if it were to expire today, it is said to be in the money; if it would be worthless if expiring with the underlying at its current price it is said to be out of the money, and if the current underlying price and strike price are equal, it is said to be at the money. There are two slightly different definitions, according to whether one uses the current price (spot) or future price (forward), specified as "at the money spot" or "at the money forward", etc.

A hedge is an investment position intended to offset potential losses or gains that may be incurred by a companion investment. A hedge can be constructed from many types of financial instruments, including stocks, exchange-traded funds, insurance, forward contracts, swaps, options, gambles, many types of over-the-counter and derivative products, and futures contracts.

In finance, a long position in a financial instrument means the holder of the position owns a positive amount of the instrument. The holder of the position has the expectation that the financial instrument will increase in value. This is known as a bullish position.

Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money.
In finance, a price (premium) is paid or received for purchasing or selling options. This article discusses the calculation of this premium in general. For further detail, see Mathematical finance § Derivatives pricing: the Q world for discussion of the mathematics, Financial engineering for the implementation, as well as Financial modeling § Quantitative finance generally.

In finance, a butterfly is a limited risk, non-directional options strategy that is designed to have a high probability of earning a limited profit when the future volatility of the underlying asset is expected to be lower or higher than that asset's current implied volatility.
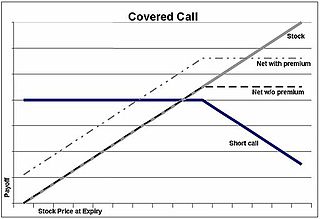
A covered call is a financial market transaction in which the seller of call options owns the corresponding amount of the underlying instrument, such as shares of a stock or other securities. If a trader buys the underlying instrument at the same time the trader sells the call, the strategy is often called a "buy-write" strategy. In equilibrium, the strategy has the same payoffs as writing a put option.

In options trading, a box spread is a combination of positions that has a certain payoff, considered to be simply "delta neutral interest rate position". For example, a bull spread constructed from calls combined with a bear spread constructed from puts has a constant payoff of the difference in exercise prices assuming that the underlying stock does not go ex-dividend before the expiration of the options. If the underlying asset has a dividend of X, then the settled value of the box will be 10 + x. Under the no-arbitrage assumption, the net premium paid out to acquire this position should be equal to the present value of the payoff.
In finance, a collar is an option strategy that limits the range of possible positive or negative returns on an underlying to a specific range. A collar strategy is used as one of the ways to hedge against possible losses and it represents long put options financed with short call options.
The iron condor is an option trading strategy utilizing two vertical spreads – a put spread and a call spread with the same expiration and four different strikes. A long iron condor is essentially selling both sides of the underlying instrument by simultaneously shorting the same number of calls and puts, then covering each position with the purchase of further out of the money call(s) and put(s) respectively. The converse produces a short iron condor.

In finance an iron butterfly, also known as the ironfly, is the name of an advanced, neutral-outlook, options trading strategy that involves buying and holding four different options at three different strike prices. It is a limited-risk, limited-profit trading strategy that is structured for a larger probability of earning smaller limited profit when the underlying stock is perceived to have a low volatility.
Option strategies are the simultaneous, and often mixed, buying or selling of one or more options that differ in one or more of the options' variables. Call options, simply known as Calls, give the buyer a right to buy a particular stock at that option's strike price. Opposite to that are Put options, simply known as Puts, which give the buyer the right to sell a particular stock at the option's strike price. This is often done to gain exposure to a specific type of opportunity or risk while eliminating other risks as part of a trading strategy. A very straightforward strategy might simply be the buying or selling of a single option; however, option strategies often refer to a combination of simultaneous buying and or selling of options.
The backspread is the converse strategy to the ratio spread and is also known as reverse ratio spread. Using calls, a bullish strategy known as the call backspread can be constructed and with puts, a strategy known as the put backspread can be constructed.

In finance, an option is a contract which conveys its owner, the holder, the right, but not the obligation, to buy or sell an underlying asset or instrument at a specified strike price prior to or on a specified date, depending on the form of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset and have a valuation that may depend on a complex relationship between underlying asset value, time until expiration, market volatility, and other factors. Options may be traded between private parties in over-the-counter (OTC) transactions, or they may be exchange-traded in live, orderly markets in the form of standardized contracts.





