Basket option

Last updated

A basket option is a financial derivative, more specifically an exotic option, whose underlying is a weighted sum or average of different assets that have been grouped together in a basket. A basket option is similar to an index option, where a number of stocks have been grouped together in an index and the option is based on the price of the index, [1] [2] but differs in that the members and weightings of an index can change over time while those in a basket option do not. [3]

Contents

Unlike a rainbow option which considers a group of assets but ultimately pays out on the level of one, a basket option is written on a basket of underlying assets but will pay out on a weighted average gain of the basket as a whole. [4]

Like rainbow options basket options are most commonly written on a basket of equity indices, though they are frequently written on a basket of individual equities as well. For example, a call option could be written on a basket of ten healthcare stocks, where the basket was composed of ten stocks in weighted proportions.

The strike price Xbasket is usually set at the current value of the basket (at-the-money), and the payoff profile will be max(Sbasket − Xbasket, 0) where Sbasket is a weighted average of n asset prices at maturity, and each weight represents the percentage of total investment in that asset. [5]

Pricing and valuation

Basket options are usually priced using an appropriate industry-standard model (such as Black–Scholes) for each individual basket component, and a matrix of correlation coefficients applied to the underlying stochastic drivers for the various models. While there are some closed-form solutions for simpler cases (e.g. two-color European rainbows), [6] semi-analytic solutions, [7] analytical approximations, [8] and numerical quadrature integrations, [9] the general case must be approached with Monte Carlo or binomial lattice methods.

Lognormality

Problems in hedging basket options can be of some significance when dealing with markets that exhibit a strong skew. Many operators price basket options as if the underlying basket were a single commodity following its own stochastic process with its volatility derived from its own time series. This however conflicts with a fact that an average (or any linear combination) of assets with lognormal distribution does not follow lognormal distribution. [10] This problem arises in swaps and Eurodollar strips (baskets of Eurodollar options) but in equities and fixed income it is mitigated by the fact that when correlation between assets is high, the sum would come closer to a lognormally distributed asset.

See also

Related Research Articles

The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments, using various underlying assumptions. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.

In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as "vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging.

In financial mathematics, the implied volatility (IV) of an option contract is that value of the volatility of the underlying instrument which, when input in an option pricing model, will return a theoretical value equal to the price of said option. A non-option financial instrument that has embedded optionality, such as an interest rate cap, can also have an implied volatility. Implied volatility, a forward-looking and subjective measure, differs from historical volatility because the latter is calculated from known past returns of a security. To understand where implied volatility stands in terms of the underlying, implied volatility rank is used to understand its implied volatility from a one-year high and low IV.

In finance, the beta is a statistic that measures the expected increase or decrease of an individual stock price in proportion to movements of the stock market as a whole. Beta can be used to indicate the contribution of an individual asset to the market risk of a portfolio when it is added in small quantity. It refers to an asset's non-diversifiable risk, systematic risk, or market risk. Beta is not a measure of idiosyncratic risk.

In mathematical finance, a Monte Carlo option model uses Monte Carlo methods to calculate the value of an option with multiple sources of uncertainty or with complicated features. The first application to option pricing was by Phelim Boyle in 1977. In 1996, M. Broadie and P. Glasserman showed how to price Asian options by Monte Carlo. An important development was the introduction in 1996 by Carriere of Monte Carlo methods for options with early exercise features.

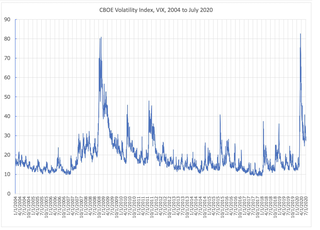
<span class="mw-page-title-main">VIX</span> Volatility index

VIX is the ticker symbol and the popular name for the Chicago Board Options Exchange's CBOE Volatility Index, a popular measure of the stock market's expectation of volatility based on S&P 500 index options. It is calculated and disseminated on a real-time basis by the CBOE, and is often referred to as the fear index or fear gauge.

In finance, a price (premium) is paid or received for purchasing or selling options. This article discusses the calculation of this premium in general. For further detail, see: Mathematical finance § Derivatives pricing: the Q world for discussion of the mathematics; Financial engineering for the implementation; as well as Financial modeling § Quantitative finance generally.

In finance, diversification is the process of allocating capital in a way that reduces the exposure to any one particular asset or risk. A common path towards diversification is to reduce risk or volatility by investing in a variety of assets. If asset prices do not change in perfect synchrony, a diversified portfolio will have less variance than the weighted average variance of its constituent assets, and often less volatility than the least volatile of its constituents.

The following outline is provided as an overview of and topical guide to finance:

In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.

In finance, a spread option is a type of option where the payoff is based on the difference in price between two underlying assets. For example, the two assets could be crude oil and heating oil; trading such an option might be of interest to oil refineries, whose profits are a function of the difference between these two prices. Spread options are generally traded over the counter, rather than on exchange.

In finance, an option is a contract which conveys to its owner, the holder, the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in over-the-counter (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts.

In finance, the Heston model, named after Steven L. Heston, is a mathematical model that describes the evolution of the volatility of an underlying asset. It is a stochastic volatility model: such a model assumes that the volatility of the asset is not constant, nor even deterministic, but follows a random process.

A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats volatility as a function of both the current asset level and of time . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant. Local volatility models are often compared with stochastic volatility models, where the instantaneous volatility is not just a function of the asset level but depends also on a new "global" randomness coming from an additional random component.

In finance, a stock market index future is a cash-settled futures contract on the value of a particular stock market index. The turnover for the global market in exchange-traded equity index futures is notionally valued, for 2008, by the Bank for International Settlements at US$130 trillion.

Rainbow option is a derivative exposed to two or more sources of uncertainty, as opposed to a simple option that is exposed to one source of uncertainty, such as the price of underlying asset.

In finance, model risk is the risk of loss resulting from using insufficiently accurate models to make decisions, originally and frequently in the context of valuing financial securities. However, model risk is more and more prevalent in activities other than financial securities valuation, such as assigning consumer credit scores, real-time probability prediction of fraudulent credit card transactions, and computing the probability of air flight passenger being a terrorist. Rebonato in 2002 defines model risk as "the risk of occurrence of a significant difference between the mark-to-model value of a complex and/or illiquid instrument, and the price at which the same instrument is revealed to have traded in the market".

Fabio Mercurio is an Italian mathematician, internationally known for a number of results in mathematical finance.

Quantitative analysis is the use of mathematical and statistical methods in finance and investment management. Those working in the field are quantitative analysts (quants). Quants tend to specialize in specific areas which may include derivative structuring or pricing, risk management, investment management and other related finance occupations. The occupation is similar to those in industrial mathematics in other industries. The process usually consists of searching vast databases for patterns, such as correlations among liquid assets or price-movement patterns.

The Bachelier model is a model of an asset price under Brownian motion presented by Louis Bachelier on his PhD thesis The Theory of Speculation. It is also called "Normal Model" equivalently.

References

  1. ↑ "Basket option". The Financial Engineer. 2014. Retrieved 14 December 2016.
  2. ↑ Hakala, Jürgen; Wystup, Uwe (2008). "FX Basket Options". Frankfurt School of Finance & Management. p. 4. Archived from the original (pdf) on 20 December 2016. Retrieved 14 December 2016.
  3. ↑ "Volatility Trading" (PDF). p. 81. Retrieved 27 September 2021.
  4. ↑ Choudhry, Moorad. Bond and money markets: strategy, trading, analysis. Butterworth-Heinemann, 2003. p.838
  5. ↑ Zhang, Peter G. Exotic options: a guide to second generation options. 1997. p553
  6. ↑ Rubinstein, Mark. "Exotic options." No. RPF-220. University of California at Berkeley, 1991. URL:http://www.haas.berkeley.edu/groups/finance/WP/rpf220.pdf Archived 2015-09-24 at the Wayback Machine
  7. ↑ Austing, Peter. Smile Pricing Explained. Springer, 2014.
  8. ↑ Alexander, C; Venkatramanan, A (2012). "Analytic Approximations for Multi-Asset Option Pricing". Mathematical Finance. 22 (4): 667–689. doi:10.1111/j.1467-9965.2011.00481.x. S2CID   73546649. SSRN   1424985.
  9. ↑ Choi, J (2018). "Sum of all Black–Scholes–Merton models: An efficient pricing method for spread, basket, and Asian options". Journal of Futures Markets . 38 (6): 627–644. arXiv: 1805.03172 . doi:10.1002/fut.21909. S2CID   59334133. SSRN   2913048.
  10. ↑ Taleb, Nassim. Dynamic hedging: managing vanilla and exotic options. Vol. 64. John Wiley & Sons, 1997. p.391
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.