
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that the curve travels counterclockwise around the point, i.e., the curve's number of turns. For certain open plane curves, the number of turns may be a non-integer. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called a parametric curve and parametric surface, respectively. In such cases, the equations are collectively called a parametric representation, or parametric system, or parameterization of the object.
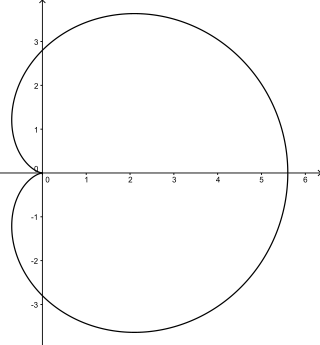
In geometry, a cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.

In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered c. 1802 by Charles Dupin, while he was still a student at the École polytechnique following Gaspard Monge's lectures. The key property of a Dupin cyclide is that it is a channel surface in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
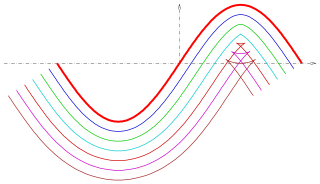
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of parallel (straight) lines. It can also be defined as a curve whose points are at a constant normal distance from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not.
In mathematics, an implicit surface is a surface in Euclidean space defined by an equation

An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that point. The osculating circle provides a way to understand the local behavior of a curve and is commonly used in differential geometry and calculus.

In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree of the dual is known as the class of the original curve. The equation of the dual of C, given in line coordinates, is known as the tangential equation of C. Duality is an involution: the dual of the dual of C is the original curve C.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.

In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
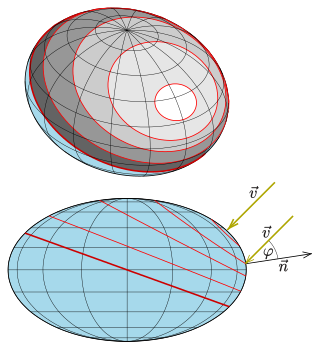
In geometry, an isophote is a curve on an illuminated surface that connects points of equal brightness. One supposes that the illumination is done by parallel light and the brightness b is measured by the following scalar product:

In geometry, an intersection is a point, line, or curve common to two or more objects. The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist. Other types of geometric intersection include:

In geometry, an intersection curve is a curve that is common to two geometric objects. In the simplest case, the intersection of two non-parallel planes in Euclidean 3-space is a line. In general, an intersection curve consists of the common points of two transversally intersecting surfaces, meaning that at any common point the surface normals are not parallel. This restriction excludes cases where the surfaces are touching or have surface parts in common.

![Implicit curve:
sin
[?]
(
x
+
y
)
-
cos
[?]
(
x
y
)
+
1
=
0
{\displaystyle \sin(x+y)-\cos(xy)+1=0} Ic-raster13-s.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Ic-raster13-s.svg/300px-Ic-raster13-s.svg.png)
![Implicit curve
sin
[?]
(
x
+
y
)
-
cos
[?]
(
x
y
)
+
1
=
0
{\displaystyle \sin(x+y)-\cos(xy)+1=0}
as level curves of the surface
z
=
sin
[?]
(
x
+
y
)
-
cos
[?]
(
x
y
)
+
1
{\displaystyle z=\sin(x+y)-\cos(xy)+1} Fl-sin-cos-nivk-s.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Fl-sin-cos-nivk-s.svg/450px-Fl-sin-cos-nivk-s.svg.png)














































































































