
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
In geometry, an equilateral polygon is a polygon which has all sides of the same length. Except in the triangle case, an equilateral polygon does not need to also be equiangular, but if it does then it is a regular polygon. If the number of sides is at least five, an equilateral polygon does not need to be a convex polygon: it could be concave or even self-intersecting.
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.
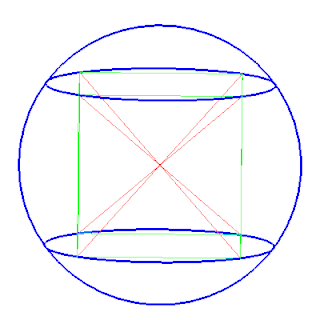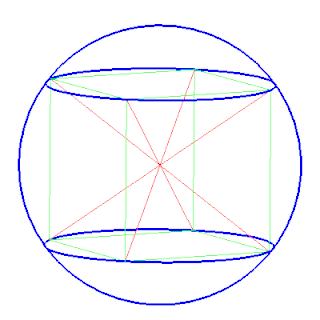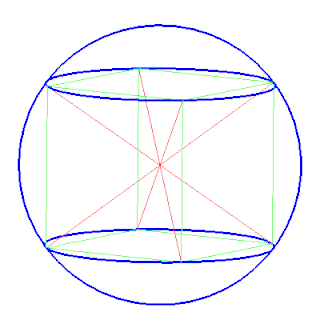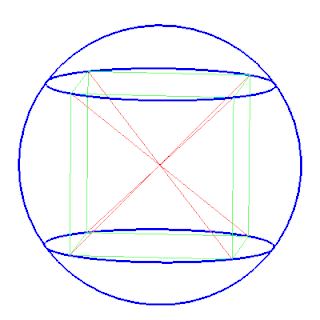
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the term circumcircle. As in the case of two-dimensional circumscribed circles (circumcircles), the radius of a sphere circumscribed around a polyhedron P is called the circumradius of P, and the center point of this sphere is called the circumcenter of P.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

In geometry, lines in a plane or higher-dimensional space are concurrent if they intersect at a single point.

In geometry, a centre or center of an object is a point in some sense in the middle of the object. According to the specific definition of centre taken into consideration, an object might have no centre. If geometry is regarded as the study of isometry groups, then a centre is a fixed point of all the isometries that move the object onto itself.
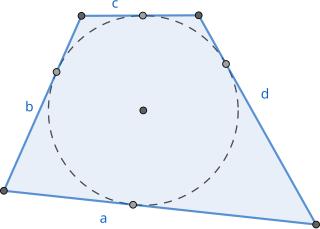
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all can be tangent to a single circle within the quadrilateral. This circle is called the incircle of the quadrilateral or its inscribed circle, its center is the incenter and its radius is called the inradius. Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals. Tangential quadrilaterals are a special case of tangential polygons.

In geometry, a bicentric polygon is a tangential polygon which is also cyclic — that is, inscribed in an outer circle that passes through each vertex of the polygon. All triangles and all regular polygons are bicentric. On the other hand, a rectangle with unequal sides is not bicentric, because no circle can be tangent to all four sides.

In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle. This is a circle that is tangent to each of the polygon's sides. The dual polygon of a tangential polygon is a cyclic polygon, which has a circumscribed circle passing through each of its vertices.
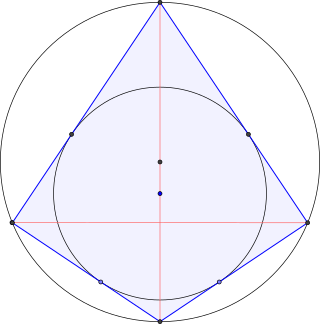
In Euclidean geometry, a right kite is a kite that can be inscribed in a circle. That is, it is a kite with a circumcircle. Thus the right kite is a convex quadrilateral and has two opposite right angles. If there are exactly two right angles, each must be between sides of different lengths. All right kites are bicentric quadrilaterals, since all kites have an incircle. One of the diagonals divides the right kite into two right triangles and is also a diameter of the circumcircle.

In mathematics and particularly in elementary geometry, a circumgon is a geometric figure which circumscribes some circle, in the sense that it is the union of the outer edges of non-overlapping triangles each of which has a vertex at the center of the circle and opposite side on a line that is tangent to the circle. The limiting case in which part or all of the circumgon is a circular arc is permitted. A circumgonal region is the union of those triangular regions.















