
In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical.

The rotation curve of a disc galaxy is a plot of the orbital speeds of visible stars or gas in that galaxy versus their radial distance from that galaxy's centre. It is typically rendered graphically as a plot, and the data observed from each side of a spiral galaxy are generally asymmetric, so that data from each side are averaged to create the curve. A significant discrepancy exists between the experimental curves observed, and a curve derived by applying gravity theory to the matter observed in a galaxy. Theories involving dark matter are the main postulated solutions to account for the variance.

In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson's equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer Lane and Robert Emden. The equation reads
A galactic halo is an extended, roughly spherical component of a galaxy which extends beyond the main, visible component. Several distinct components of a galaxy comprise its halo:

The Friedmann equations, also known as the Friedmann–Lemaître (FL) equations, are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density ρ and pressure p. The equations for negative spatial curvature were given by Friedmann in 1924.
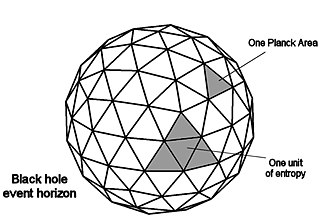
In physics, the Bekenstein bound is an upper limit on the thermodynamic entropy S, or Shannon entropy H, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximum amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy are finite.

In modern models of physical cosmology, a dark matter halo is a basic unit of cosmological structure. It is a hypothetical region that has decoupled from cosmic expansion and contains gravitationally bound matter. A single dark matter halo may contain multiple virialized clumps of dark matter bound together by gravity, known as subhalos. Modern cosmological models, such as ΛCDM, propose that dark matter halos and subhalos may contain galaxies. The dark matter halo of a galaxy envelops the galactic disc and extends well beyond the edge of the visible galaxy. Thought to consist of dark matter, halos have not been observed directly. Their existence is inferred through observations of their effects on the motions of stars and gas in galaxies and gravitational lensing. Dark matter halos play a key role in current models of galaxy formation and evolution. Theories that attempt to explain the nature of dark matter halos with varying degrees of success include cold dark matter (CDM), warm dark matter, and massive compact halo objects (MACHOs).

A satellite galaxy is a smaller companion galaxy that travels on bound orbits within the gravitational potential of a more massive and luminous host galaxy. Satellite galaxies and their constituents are bound to their host galaxy, in the same way that planets within the Solar System are gravitationally bound to the Sun. While most satellite galaxies are dwarf galaxies, satellite galaxies of large galaxy clusters can be much more massive. The Milky Way is orbited by about fifty satellite galaxies, the largest of which is the Large Magellanic Cloud.
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space. Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems.
In probability theory and statistics, the Jensen–Shannon divergence, named after Johan Jensen and Claude Shannon, is a method of measuring the similarity between two probability distributions. It is also known as information radius (IRad) or total divergence to the average. It is based on the Kullback–Leibler divergence, with some notable differences, including that it is symmetric and it always has a finite value. The square root of the Jensen–Shannon divergence is a metric often referred to as Jensen–Shannon distance. The similarity between the distributions is greater when the Jensen-Shannon distance is closer to zero.

The Jeans instability is a concept in astrophysics that describes an instability that leads to the gravitational collapse of a cloud of gas or dust. It causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent the gravitational collapse of a region filled with matter. It is named after James Jeans.

In condensed-matter physics, channelling (or channeling) is the process that constrains the path of a charged particle in a crystalline solid.

In physics, the Lemaître–Tolman metric, also known as the Lemaître–Tolman–Bondi metric or the Tolman metric, is a Lorentzian metric based on an exact solution of Einstein's field equations; it describes an isotropic and expanding universe which is not homogeneous, and is thus used in cosmology as an alternative to the standard Friedmann–Lemaître–Robertson–Walker metric to model the expansion of the universe. It has also been used to model a universe which has a fractal distribution of matter to explain the accelerating expansion of the universe. It was first found by Georges Lemaître in 1933 and Richard Tolman in 1934 and later investigated by Hermann Bondi in 1947.

The Sérsic profile is a mathematical function that describes how the intensity of a galaxy varies with distance from its center. It is a generalization of de Vaucouleurs' law. José Luis Sérsic first published his law in 1963.
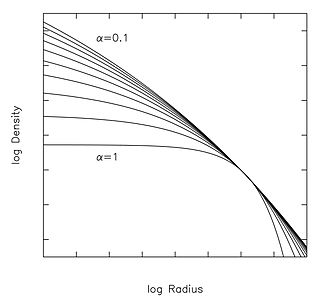
The Einasto profile is a mathematical function that describes how the density of a spherical stellar system varies with distance from its center. Jaan Einasto introduced his model at a 1963 conference in Alma-Ata, Kazakhstan.

In cosmology, baryon acoustic oscillations (BAO) are fluctuations in the density of the visible baryonic matter of the universe, caused by acoustic density waves in the primordial plasma of the early universe. In the same way that supernovae provide a "standard candle" for astronomical observations, BAO matter clustering provides a "standard ruler" for length scale in cosmology. The length of this standard ruler is given by the maximum distance the acoustic waves could travel in the primordial plasma before the plasma cooled to the point where it became neutral atoms, which stopped the expansion of the plasma density waves, "freezing" them into place. The length of this standard ruler can be measured by looking at the large scale structure of matter using astronomical surveys. BAO measurements help cosmologists understand more about the nature of dark energy by constraining cosmological parameters.
In astrophysics, the virial mass is the mass of a gravitationally bound astrophysical system, assuming the virial theorem applies. In the context of galaxy formation and dark matter halos, the virial mass is defined as the mass enclosed within the virial radius of a gravitationally bound system, a radius within which the system obeys the virial theorem. The virial radius is determined using a "top-hat" model. A spherical "top hat" density perturbation destined to become a galaxy begins to expand, but the expansion is halted and reversed due to the mass collapsing under gravity until the sphere reaches equilibrium – it is said to be virialized. Within this radius, the sphere obeys the virial theorem which says that the average kinetic energy is equal to minus one half times the average potential energy, , and this radius defines the virial radius.

The Jeans equations are a set of partial differential equations that describe the motion of a collection of stars in a gravitational field. The Jeans equations relate the second-order velocity moments to the density and potential of a stellar system for systems without collision. They are analogous to the Euler equations for fluid flow and may be derived from the collisionless Boltzmann equation. The Jeans equations can come in a variety of different forms, depending on the structure of what is being modelled. Most utilization of these equations has been found in simulations with large number of gravitationally bound objects.
The Ellis drainhole is the earliest-known complete mathematical model of a traversable wormhole. It is a static, spherically symmetric solution of the Einstein vacuum field equations augmented by inclusion of a scalar field minimally coupled to the geometry of space-time with coupling polarity opposite to the orthodox polarity :
The spherical collapse model describes the evolution of nearly homogeneous matter in the early Universe into collapsed virialized structures - dark matter halos. This model assumes that halos are spherical and dominated by gravity which leads to an analytical solution for several of the halos' properties such as density and radius over time.












































