Rosenbrock methods refers to either of two distinct ideas in numerical computation, both named for Howard H. Rosenbrock.
Rosenbrock methods refers to either of two distinct ideas in numerical computation, both named for Howard H. Rosenbrock.
Rosenbrock methods for stiff differential equations are a family of single-step methods for solving ordinary differential equations. [1] [2] They are related to the implicit Runge–Kutta methods [3] and are also known as Kaps–Rentrop methods. [4]
Rosenbrock search is a numerical optimization algorithm applicable to optimization problems in which the objective function is inexpensive to compute and the derivative either does not exist or cannot be computed efficiently. [5] The idea of Rosenbrock search is also used to initialize some root-finding routines, such as fzero (based on Brent's method) in Matlab. Rosenbrock search is a form of derivative-free search but may perform better on functions with sharp ridges. [6] The method often identifies such a ridge which, in many applications, leads to a solution. [7]

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.
A computer algebra system (CAS) or symbolic algebra system (SAS) is any mathematical software with the ability to manipulate mathematical expressions in a way similar to the traditional manual computations of mathematicians and scientists. The development of the computer algebra systems in the second half of the 20th century is part of the discipline of "computer algebra" or "symbolic computation", which has spurred work in algorithms over mathematical objects such as polynomials.
In computational intelligence (CI), an evolutionary algorithm (EA) is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions. Evolution of the population then takes place after the repeated application of the above operators.

Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term can also refer to the computation of integrals.
Computational science, also known as scientific computing, technical computing or scientific computation (SC), is a division of science that uses advanced computing capabilities to understand and solve complex physical problems. This includes
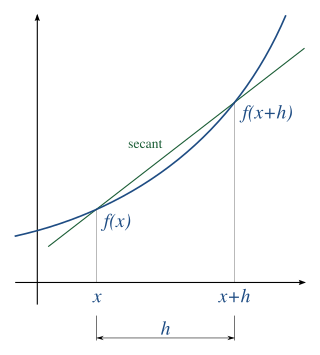
In numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
In mathematics, a differential-algebraic system of equations (DAE) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.
Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations,
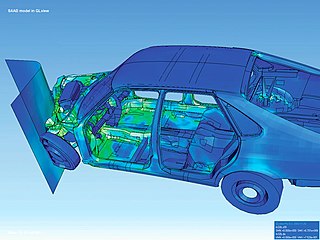
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.

In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with other DE, its unknown(s) consists of one function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equations (PDEs) which may be with respect to more than one independent variable, and, less commonly, in contrast with stochastic differential equations (SDEs) where the progression is random.
The following is a timeline of numerical analysis after 1945, and deals with developments after the invention of the modern electronic computer, which began during Second World War. For a fuller history of the subject before this period, see timeline and history of mathematics.
Exponential integrators are a class of numerical methods for the solution of ordinary differential equations, specifically initial value problems. This large class of methods from numerical analysis is based on the exact integration of the linear part of the initial value problem. Because the linear part is integrated exactly, this can help to mitigate the stiffness of a differential equation. Exponential integrators can be constructed to be explicit or implicit for numerical ordinary differential equations or serve as the time integrator for numerical partial differential equations.
PROSE was the mathematical 4GL virtual machine that established the holistic modeling paradigm known as Synthetic Calculus. A successor to the SLANG/CUE simulation and optimization language developed at TRW Systems, it was introduced in 1974 on Control Data supercomputers. It was the first commercial language to employ automatic differentiation (AD), which was optimized to loop in the instruction-stack of the CDC 6600 CPU.
Fluid motion is governed by the Navier–Stokes equations, a set of coupled and nonlinear partial differential equations derived from the basic laws of conservation of mass, momentum and energy. The unknowns are usually the flow velocity, the pressure and density and temperature. The analytical solution of this equation is impossible hence scientists resort to laboratory experiments in such situations. The answers delivered are, however, usually qualitatively different since dynamical and geometric similitude are difficult to enforce simultaneously between the lab experiment and the prototype. Furthermore, the design and construction of these experiments can be difficult, particularly for stratified rotating flows. Computational fluid dynamics (CFD) is an additional tool in the arsenal of scientists. In its early days CFD was often controversial, as it involved additional approximation to the governing equations and raised additional (legitimate) issues. Nowadays CFD is an established discipline alongside theoretical and experimental methods. This position is in large part due to the exponential growth of computer power which has allowed us to tackle ever larger and more complex problems.
Validated numerics, or rigorous computation, verified computation, reliable computation, numerical verification is numerics including mathematically strict error evaluation, and it is one field of numerical analysis. For computation, interval arithmetic is used, and all results are represented by intervals. Validated numerics were used by Warwick Tucker in order to solve the 14th of Smale's problems, and today it is recognized as a powerful tool for the study of dynamical systems.
Probabilistic numerics is an active field of study at the intersection of applied mathematics, statistics, and machine learning centering on the concept of uncertainty in computation. In probabilistic numerics, tasks in numerical analysis such as finding numerical solutions for integration, linear algebra, optimization and simulation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.
{{cite web}}: CS1 maint: archived copy as title (link)