In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.

In hyperbolic geometry, the order-5 dodecahedral honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {5,3,5}, it has five dodecahedral cells around each edge, and each vertex is surrounded by twenty dodecahedra. Its vertex figure is an icosahedron.

In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure.

In geometry, a dodecahedral prism is a convex uniform 4-polytope. This 4-polytope has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In geometry, an icosahedral prism is a convex uniform 4-polytope. This 4-polytope has 22 polyhedral cells: 2 icosahedra connected by 20 triangular prisms. It has 70 faces: 30 squares and 40 triangles. It has 72 edges and 24 vertices.
In 4-dimensional geometry, a truncated octahedral prism or omnitruncated tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 cells It has 64 faces, and 96 edges and 48 vertices.

In geometry, a truncated dodecahedral prism is a convex uniform polychoron.
In geometry, a rhombicuboctahedral prism is a convex uniform polychoron.

In geometry, a truncated cuboctahedral prism or great rhombicuboctahedral prism is a convex uniform polychoron.
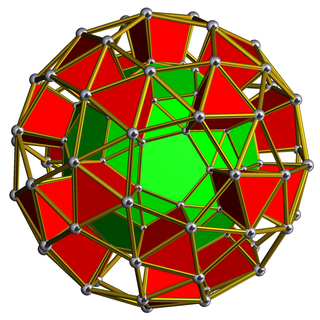
In geometry, a snub dodecahedral prism or snub icosidodecahedral prism is a convex uniform polychoron.

In four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball of radius r1 and a line segment of length 2r2:

In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere, a flat plane in hyperbolic space that approaches a single ideal point at infinity.