Relation to Kt/V
Mathematically, the URR is closely related to Kt/V, and the two quantities can be derived from another with more or less precision, depending on the amount of additional information available about a given dialysis session.
Kt/V is one of the reference methods by which the amount of dialysis given is measured. Kt/V, like the URR, focuses on urea as the target solute, and is based on the assumption that removal of urea is from a single space – urea distribution volume, or  similar in capacity to the total body water. The urea distribution volume
similar in capacity to the total body water. The urea distribution volume  , although traditionally thought of as 60% of body weight, may actually be closer to 50% of the body weight in women and 55% in men with stage V (GFR < 15 ml/min) chronic kidney disease. The clearance of urea during the dialysis session
, although traditionally thought of as 60% of body weight, may actually be closer to 50% of the body weight in women and 55% in men with stage V (GFR < 15 ml/min) chronic kidney disease. The clearance of urea during the dialysis session  can be expressed in either
can be expressed in either  or
or  .
.
Time or  is the duration of the dialysis session, measured either in minutes or hours. So
is the duration of the dialysis session, measured either in minutes or hours. So  is also a volume, either
is also a volume, either  , or
, or  , and represents the volume of blood (in ml or L) cleared of urea during the dialysis session. Because
, and represents the volume of blood (in ml or L) cleared of urea during the dialysis session. Because  is also a volume, the ratio of
is also a volume, the ratio of  has dimensions of
has dimensions of  or
or  , making it a "dimensionless" ratio.
, making it a "dimensionless" ratio.
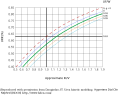
In a simplified model of urea removal from a fixed volume with no urea generation,  is related to
is related to  by the following relationship:
by the following relationship:

Actually, this relationship is made a bit more complex by the fact that fluid is removed during dialysis, so the removal space V shrinks, and because a small amount of urea is generated during the dialysis session. Both of these factors make the actual post-dialysis serum urea level higher than expected, and the URR lower than expected, when the extremely simplified equation above, is used.
A more accurate relationship between URR and Kt/V can be derived by single-pool, variable volume urea kinetic modeling. A simplified estimating equation also can be used. [2] This gives results that are quite similar to formal urea modeling as long as dialysis treatments of 2–6 hours in duration are given, and Kt/V is between 0.7 and 2.0.

The  term is a function of the dialysis session duration (t), and adjusts for the amount of urea generated during the dialysis session. The second term,
term is a function of the dialysis session duration (t), and adjusts for the amount of urea generated during the dialysis session. The second term,  adjusts for the additional urea that is cleared from the body through volume contraction.
adjusts for the additional urea that is cleared from the body through volume contraction.
Because  can be approximated by
can be approximated by  , where UF = ultrafiltrate removed during dialysis (estimated as the weight lost during the treatment) and W = postdialysis body weight, and because dialysis sessions given 3 times per week are usually about 3.5 hours long, the above equation can be simplified to:
, where UF = ultrafiltrate removed during dialysis (estimated as the weight lost during the treatment) and W = postdialysis body weight, and because dialysis sessions given 3 times per week are usually about 3.5 hours long, the above equation can be simplified to:

Limitations of URR vs. Kt/V
The URR is designed to measure the amount of dialysis given when the dialysis clearance of urea greatly exceeds the urea generation rate. In continuous hemodialysis or in peritoneal dialysis, for example, a considerable amount of dialysis is delivered, but the urea level remains roughly constant after the initial treatment of uremia, so the URR is essentially zero. In long slow overnight dialysis, if simplified equations are used, the URR also underestimates the amount of dialysis due to urea generation during the long dialytic session. For this reason, the kinetically modeled Kt/V is always recommended as the best measure of dialysis adequacy. The Kt/V, even that derived by formal modeling, is primarily based on the URR, and so it contains little additional information in terms of the amount of dialysis that was delivered. Since the URR and Kt/V are so closely related, their predictive power in terms of patient outcome is similar. However, use of Kt/V and urea modeling in general allows for comparing expected with predicted dose of dialysis, which can be used to analyze dialysis treatments and dialyzer clearances and in troubleshooting and quality control activities. Also, Kt/V permits calculation of the urea generation rate, which can give clues about a patient's protein intake.