The guitar is a fretted musical instrument that typically has six strings. It is held flat against the player's body and played by strumming or plucking the strings with the dominant hand, while simultaneously pressing the strings against frets with the fingers of the opposite hand. A plectrum or individual finger picks may be used to strike the strings. The sound of the guitar is projected either acoustically, by means of a resonant chamber on the instrument, or amplified by an electronic pickup and an amplifier.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B. According to this definition, within a diatonic scale there is only one tritone for each octave. For instance, the above-mentioned interval F–B is the only tritone formed from the notes of the C major scale. A tritone is also commonly defined as an interval spanning six semitones. According to this definition, a diatonic scale contains two tritones for each octave. For instance, the above-mentioned C major scale contains the tritones F–B and B–F. In twelve-equal temperament, the tritone divides the octave exactly in half as 6 of 12 semitones or 600 of 1200 cents.

In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.

Among guitar tunings, all-fifths tuning refers to the set of tunings in which each interval between consecutive open strings is a perfect fifth. All-fifths tuning is also called fifths, perfect fifths, or mandoguitar. The conventional "standard tuning" consists of perfect fourths and a single major third between the g and b strings:

In music, a guitar chord is a set of notes played on a guitar. A chord's notes are often played simultaneously, but they can be played sequentially in an arpeggio. The implementation of guitar chords depends on the guitar tuning. Most guitars used in popular music have six strings with the "standard" tuning of the Spanish classical guitar, namely E-A-D-G-B-E' ; in standard tuning, the intervals present among adjacent strings are perfect fourths except for the major third (G,B). Standard tuning requires four chord-shapes for the major triads.

Guitar tunings are the assignment of pitches to the open strings of guitars, including acoustic guitars, electric guitars, and classical guitars. Tunings are described by the particular pitches that are made by notes in Western music. By convention, the notes are ordered and arranged from the lowest-pitched string to the highest-pitched string, or the thickest string to thinnest, or the lowest frequency to the highest. This sometimes confuses beginner guitarists, since the highest-pitched string is referred to as the 1st string, and the lowest-pitched is the 6th string.
Jazz chords refer to chords, chord voicings and chord symbols that jazz musicians commonly use in composition, improvisation, and harmony. In jazz chords and theory, most triads that appear in lead sheets or fake books can have sevenths added to them, using the performer's discretion and ear. For example, if a tune is in the key of C, if there is a G chord, the chord-playing performer usually voices this chord as G7. While the notes of a G7 chord are G–B–D–F, jazz often omits the fifth of the chord—and even the root if playing in a group. However, not all jazz pianists leave out the root when they play voicings: Bud Powell, one of the best-known of the bebop pianists, and Horace Silver, whose quintet included many of jazz's biggest names from the 1950s to the 1970s, included the root note in their voicings.
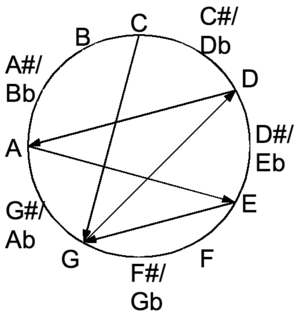
New standard tuning (NST) is an alternative tuning for the guitar that approximates all-fifths tuning. The guitar's strings are assigned the notes C2-G2-D3-A3-E4-G4 ; the five lowest open strings are each tuned to an interval of a perfect fifth {(C,G),(G,D),(D,A),(A,E)}; the two highest strings are a minor third apart (E,G).

Among alternative tunings for the guitar, an open G tuning is an open tuning that features the G-major chord; its open notes are selected from the notes of a G-major chord, such as the G-major triad (G,B,D). For example, a popular open-G tuning is

Open C tuning is an open tuning for guitar. The open-string notes form a C major chord, which is the triad (C,E,G) having the root note C, the major third (C,E), and the perfect fifth (C,G). When the guitar is strummed without fretting any strings, a C-major chord is sounded. By barring all of the strings for one fret, one finger suffices to fret the other eleven major-chords.

Among alternative tunings for the guitar, all-fourths tuning is a regular tuning. In contrast, the standard tuning has one irregularity—a major third between the third and second strings—while having perfect fourths between the other successive strings. The standard tuning's irregular major-third is replaced by a perfect fourth in all-fourths tuning, which has the open notes E2-A2-D3-G3-C4-F4.
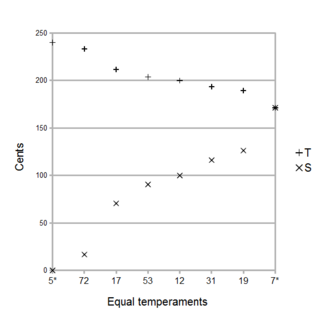
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

Among alternative tunings for guitar, a major-thirds tuning is a regular tuning in which each interval between successive open strings is a major third. Other names for major-thirds tuning include major-third tuning, M3 tuning, all-thirds tuning, and augmented tuning. By definition, a major-third interval separates two notes that differ by exactly four semitones.

Among alternative guitar-tunings, regular tunings have equal musical intervals between the paired notes of their successive open strings.

Repetitive tunings are alternative tunings for the guitar. A repetitive tuning begins with a list of notes that is duplicated, either at unison or at higher octaves.

Among alternative tunings for the guitar, an overtones tuning selects its open-string notes from the overtone sequence of a fundamental note. An example is the open tuning constituted by the first six overtones of the fundamental note C, namely C2-C3-G3-C4-E4-G4.