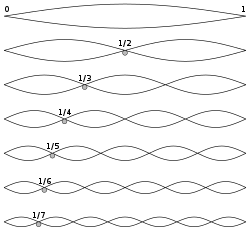
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

In music, there are two common meanings for tuning:
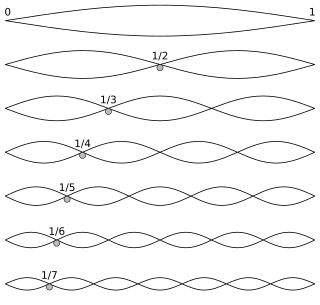
An overtone is any resonant frequency above the fundamental frequency of a sound. In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.

Meantone temperaments are musical temperaments, that is a variety of tuning systems, obtained by narrowing the fifths so that their ratio is slightly less than 3:2, in order to push the thirds closer to pure. Meantone temperaments are constructed similarly to Pythagorean tuning, as a stack of equal fifths, but they are temperaments in that the fifths are not pure.

A power chord is a colloquial name for a chord in guitar music, especially electric guitar, that consists of the root note and the fifth, as well as possibly octaves of those notes. Power chords are commonly played on amplified guitars, especially on electric guitar with intentionally added distortion or overdrive effects. Power chords are a key element of many styles of rock, especially heavy metal and punk rock.
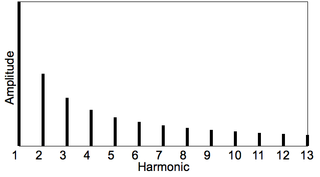
In music, inharmonicity is the degree to which the frequencies of overtones depart from whole multiples of the fundamental frequency.

An eight-string guitar is a guitar with eight strings, or one more than the Russian guitar's seven. Eight-string guitars are less common than six- and seven-string guitars, but they are used by a few classical, jazz, and metal guitarists. The eight-string guitar allows a wider tonal range, or non-standard tunings, or both.

Among guitar tunings, all-fifths tuning refers to the set of tunings in which each interval between consecutive open strings is a perfect fifth. All-fifths tuning is also called fifths, perfect fifths, or mandoguitar. The conventional "standard tuning" consists of perfect fourths and a single major third between the g and b strings:

In music, a guitar chord is a set of notes played on a guitar. A chord's notes are often played simultaneously, but they can be played sequentially in an arpeggio. The implementation of guitar chords depends on the guitar tuning. Most guitars used in popular music have six strings with the "standard" tuning of the Spanish classical guitar, namely E–A–D–G–B–E' ; in standard tuning, the intervals present among adjacent strings are perfect fourths except for the major third (G,B). Standard tuning requires four chord-shapes for the major triads.

Guitar tunings are the assignment of pitches to the open strings of guitars, including classical guitars, acoustic guitars, and electric guitars. Tunings are described by the particular pitches that are made by notes in Western music. By convention, the notes are ordered and arranged from the lowest-pitched string to the highest-pitched string, or the thickest string to thinnest, or the lowest frequency to the highest. This sometimes confuses beginner guitarists, since the highest-pitched string is referred to as the 1st string, and the lowest-pitched is the 6th string.

New standard tuning (NST) is an alternative tuning for the guitar that approximates all-fifths tuning. The guitar's strings are assigned the notes C2-G2-D3-A3-E4-G4 ; the five lowest open strings are each tuned to an interval of a perfect fifth {(C,G),(G,D),(D,A),(A,E)}; the two highest strings are a minor third apart (E,G).
In music, intonation is the pitch accuracy of a musician or musical instrument. Intonation may be flat, sharp, or both, successively or simultaneously.
Among alternative tunings for the guitar, an open G tuning is an open tuning that features the G-major chord; its open notes are selected from the notes of a G-major chord, such as the G-major triad (G,B,D). For example, a popular open-G tuning is

Open C tuning is an open tuning for guitar. The open-string notes form a C major chord, which is the triad (C,E,G) having the root note C, the major third (C,E), and the perfect fifth (C,G). When the guitar is strummed without fretting any strings, a C-major chord is sounded. By barring all of the strings for one fret, one finger suffices to fret the other eleven major-chords.

Among alternative tunings for guitar, a major-thirds tuning is a regular tuning in which each interval between successive open strings is a major third. Other names for major-thirds tuning include major-third tuning, M3 tuning, all-thirds tuning, and augmented tuning. By definition, a major-third interval separates two notes that differ by exactly four semitones.

Among alternative tunings for guitar, each augmented-fourths tuning is a regular tuning in which the musical intervals between successive open-string notes are each augmented fourths. Because augmented fourths are alternatively called "tritones" ("tri-tones") or "diminished fifths", augmented-fourths tuning is also called tritone tuning or diminished-fifths tuning.

Among alternative guitar-tunings, regular tunings have equal musical intervals between the paired notes of their successive open strings.

Repetitive tunings are a type of alternative tunings for the guitar. A repetitive tuning begins with a list of notes that is duplicated, either at unison or at higher octaves.