In music, an octave or perfect octave is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In music theory, the tritone is defined as a musical interval spanning three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.

A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth is the fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, because the note F is the fifth semitone above C, and there are four staff positions between C and F. Diminished and augmented fourths span the same number of staff positions, but consist of a different number of semitones.

In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C♯; the interval between them is a semitone.

In classical music, a third is a musical interval encompassing three staff positions, and the major third is a third spanning four semitones. Along with the minor third, the major third is one of two commonly occurring thirds. It is qualified as major because it is the larger of the two: the major third spans four semitones, the minor third three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones.
The intervals from the tonic (keynote) in an upward direction to the second, to the third, to the sixth, and to the seventh scale degrees of a major scale are called major.

In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions. The minor third is one of two commonly occurring thirds. It is called minor because it is the smaller of the two: the major third spans an additional semitone. For example, the interval from A to C is a minor third, as the note C lies three semitones above A. Coincidentally, there are three staff positions from A to C. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones. The minor third is a skip melodically.
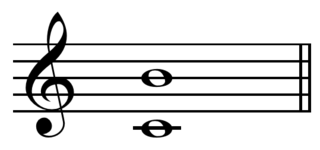
In music from Western culture, a seventh is a musical interval encompassing seven staff positions, and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two. The major seventh spans eleven semitones, its smaller counterpart being the minor seventh, spanning ten semitones. For example, the interval from C to B is a major seventh, as the note B lies eleven semitones above C, and there are seven staff positions from C to B. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones.
The intervals from the tonic (keynote) in an upward direction to the second, to the third, to the sixth, and to the seventh scale degrees (of a major scale are called major.

In Western music and music theory, diminution has four distinct meanings. Diminution may be a form of embellishment in which a long note is divided into a series of shorter, usually melodic, values. Diminution may also be the compositional device where a melody, theme or motif is presented in shorter note-values than were previously used. Diminution is also the term for the proportional shortening of the value of individual note-shapes in mensural notation, either by coloration or by a sign of proportion. A minor or perfect interval that is narrowed by a chromatic semitone is a diminished interval, and the process may be referred to as diminution.

In music, a ninth is a compound interval consisting of an octave plus a second.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
Jazz chords are chords, chord voicings and chord symbols that jazz musicians commonly use in composition, improvisation, and harmony. In jazz chords and theory, most triads that appear in lead sheets or fake books can have sevenths added to them, using the performer's discretion and ear. For example, if a tune is in the key of C, if there is a G chord, the chord-playing performer usually voices this chord as G7. While the notes of a G7 chord are G–B–D–F, jazz often omits the fifth of the chord—and even the root if playing in a group. However, not all jazz pianists leave out the root when they play voicings: Bud Powell, one of the best-known of the bebop pianists, and Horace Silver, whose quintet included many of jazz's biggest names from the 1950s to the 1970s, included the root note in their voicings.
Quarter-comma meantone, or 1⁄4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81 : 80), with respect to its just intonation used in Pythagorean tuning ; the result is 3/2 × 1⁄4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.
In modern Western tonal music theory an augmented unison or augmented prime is the interval between two notes on the same staff position, or denoted by the same note letter, whose alterations cause them, in ordinary equal temperament, to be one semitone apart. In other words, it is a unison where one note has been altered by a half-step, such as B♭ and B♮ or C♮ and C♯. The interval is often described as a chromatic semitone. The term, in its French form unisson superflu, appears to have been coined by Jean-Philippe Rameau in 1722, who also called this interval a minor semitone. Historically, this interval, like the tritone, is described as being "mi contra fa", and therefore is the "diabolus in musica". In 12-tone equal temperament, it is the enharmonic equivalent of a diatonic semitone or minor second, although in other tunings the diatonic semitone is a different interval.

In modern Western tonal music theory, a diminished second is the interval produced by narrowing a minor second by one chromatic semitone. It is enharmonically equivalent to a perfect unison. Thus, it is the interval between notes on two adjacent staff positions, or having adjacent note letters, altered in such a way that they have no pitch difference in twelve-tone equal temperament. An example is the interval from a B to the C♭ immediately above; another is the interval from a B♯ to the C immediately above.

Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.

Among alternative guitar-tunings, regular tunings have equal musical intervals between the paired notes of their successive open strings.













