Related Research Articles
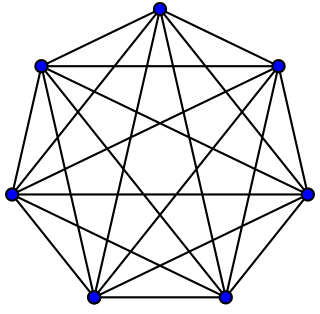
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.
In the mathematical field of graph theory, an automorphism is a permutation of the vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices v1 and v2 of G, there is an automorphism f such that

In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.
In mathematics, a universal graph is an infinite graph that contains every finite graph as an induced subgraph. A universal graph of this type was first constructed by Richard Rado and is now called the Rado graph or random graph. More recent work has focused on universal graphs for a graph family F: that is, an infinite graph belonging to F that contains all finite graphs in F. For instance, the Henson graphs are universal in this sense for the i-clique-free graphs.
George Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor emeritus at the Ohio State University.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
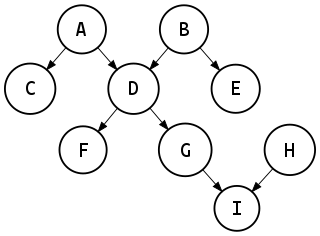
In mathematics, and more specifically in graph theory, a polytree is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is both connected and acyclic.

In graph theory, the Kneser graphK(n, k) (alternatively KGn,k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1956.

Imre Bennett Leader is a British mathematician, a professor in DPMMS at the University of Cambridge working in the field of combinatorics. He is also known as an Othello player.

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

Maria Chudnovsky is an Israeli-American mathematician working on graph theory and combinatorial optimization. She is a 2012 MacArthur Fellow.
Combinatorica is an international journal of mathematics, publishing papers in the fields of combinatorics and computer science. It started in 1981, with László Babai and László Lovász as the editors-in-chief with Paul Erdős as honorary editor-in-chief. The current editors-in-chief are Imre Bárány and József Solymosi. The advisory board consists of Ronald Graham, Gyula O. H. Katona, Miklós Simonovits, Vera Sós, and Endre Szemerédi. It is published by the János Bolyai Mathematical Society and Springer Verlag.

In graph theory, a branch of mathematics, a Hamiltonian decomposition of a given graph is a partition of the edges of the graph into Hamiltonian cycles. Hamiltonian decompositions have been studied both for undirected graphs and for directed graphs. In the undirected case a Hamiltonian decomposition can also be described as a 2-factorization of the graph such that each factor is connected.

Sumner's conjecture states that every orientation of every -vertex tree is a subgraph of every -vertex tournament. David Sumner, a graph theorist at the University of South Carolina, conjectured in 1971 that tournaments are universal graphs for polytrees. The conjecture was proven for all large by Daniela Kühn, Richard Mycroft, and Deryk Osthus.
The European Prize in Combinatorics is a prize for research in combinatorics, a mathematical discipline, which is awarded biennially at Eurocomb, the European conference on combinatorics, graph theory, and applications. The prize was first awarded at Eurocomb 2003 in Prague. Recipients must not be older than 35. The most recent prize was awarded at Eurocomb 2023 in Prague.

In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if is a 2-vertex-connected graph, then the square of is Hamiltonian. It is named after Herbert Fleischner, who published its proof in 1974.
Deryk Osthus is the Professor of Graph Theory at the School of Mathematics, University of Birmingham. He is known for his research in combinatorics, predominantly in extremal and probabilistic graph theory.
David P. Sumner is an American mathematician known for his research in graph theory. He formulated Sumner's conjecture that tournaments are universal graphs for polytrees in 1971, and showed in 1974 that all claw-free graphs with an even number of vertices have perfect matchings. He and András Gyárfás independently formulated the Gyárfás–Sumner conjecture according to which, for every tree T, the T-free graphs are χ-bounded.
References
- ↑ Birth year from ISNI authority control file, retrieved 2018-11-28.
- 1 2 3 Staff profile, University of Birmingham School of Mathematics, accessed 2012-09-12.
- ↑ Daniela Kühn at the Mathematics Genealogy Project
- ↑ Diestel, Reinhard; Kühn, Daniela (2004), "On infinite cycles. I, II.", Combinatorica, 24 (1): 69–89 & 91–116, doi:10.1007/s00493-004-0005-z, MR 2057684, S2CID 15797002 . See in particular Richter's review in the MR link.
- ↑ Kühn, Daniela; Mycroft, Richard; Osthus, Deryk (2011), "A proof of Sumner's universal tournament conjecture for large tournaments", Proceedings of the London Mathematical Society , Third Series, 102 (4): 731–766, arXiv: 1010.4430 , doi:10.1112/plms/pdq035, MR 2793448, S2CID 119169562, Zbl 1218.05034 .
- ↑ Richard-Rado-Preis Archived 2013-01-06 at archive.today (in German), Fachgruppe Diskrete Mathematik, DMV, accessed 2012-09-12.
- ↑ "Awards" (PDF), European Mathematical Society Newsletter, 50: 24, December 2003.
- ↑ "LMS Prizes 2014". London Mathematical Society. Retrieved 7 August 2014.
- ↑ "ICM Plenary and Invited Speakers since 1897". International Mathematical Union (IMU). 2015-09-27. Archived from the original on 2017-11-08. Retrieved 2015-09-27.
- ↑ "Royal Society announces recipients of prestigious Wolfson Research Merit Awards". Royal Society. 31 July 2015. Retrieved 2015-09-27.
- ↑ "Professor Daniela Kühn FRS". Royal Society. Retrieved 2024-05-20.