Related Research Articles
In ontology, the theory of categories concerns itself with the categories of being: the highest genera or kinds of entities according to Amie Thomasson. To investigate the categories of being, or simply categories, is to determine the most fundamental and the broadest classes of entities. A distinction between such categories, in making the categories or applying them, is called an ontological distinction. Various systems of categories have been proposed, they often include categories for substances, properties, relations, states of affairs or events. A representative question within the theory of categories might articulate itself, for example, in a query like, "Are universals prior to particulars?"

A definition is a statement of the meaning of a term. Definitions can be classified into two large categories: intensional definitions, and extensional definitions. Another important category of definitions is the class of ostensive definitions, which convey the meaning of a term by pointing out examples. A term may have many different senses and multiple meanings, and thus require multiple definitions.

In metaphysics, nominalism is the view that universals and abstract objects do not actually exist other than being merely names or labels. There are at least two main versions of nominalism. One version denies the existence of universals – things that can be instantiated or exemplified by many particular things. The other version specifically denies the existence of abstract objects – objects that do not exist in space and time.

In metaphysics, ontology is the philosophical study of being. It investigates what types of entities exist, how they are grouped into categories, and how they are related to one another on the most fundamental level. Ontologists often try to determine what the categories or highest kinds are and how they form a system of categories that encompasses the classification of all entities. Commonly proposed categories include substances, properties, relations, states of affairs, and events. These categories are characterized by fundamental ontological concepts, including particularity and universality, abstractness and concreteness, or possibility and necessity. Of special interest is the concept of ontological dependence, which determines whether the entities of a category exist on the most fundamental level. Disagreements within ontology are often about whether entities belonging to a certain category exist and, if so, how they are related to other entities.

The problem of universals is an ancient question from metaphysics that has inspired a range of philosophical topics and disputes: "Should the properties an object has in common with other objects, such as color and shape, be considered to exist beyond those objects? And if a property exists separately from objects, what is the nature of that existence?"
Substance theory, or substance–attribute theory, is an ontological theory positing that objects are constituted each by a substance and properties borne by the substance but distinct from it. In this role, a substance can be referred to as a substratum or a thing-in-itself. Substances are particulars that are ontologically independent: they are able to exist all by themselves. Another defining feature often attributed to substances is their ability to undergo changes. Changes involve something existing before, during and after the change. They can be described in terms of a persisting substance gaining or losing properties. Attributes or properties, on the other hand, are entities that can be exemplified by substances. Properties characterize their bearers; they express what their bearer is like.

A syllogism is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true.
In formal semantics, an ontological commitment of a language is one or more objects postulated to exist by that language. The 'existence' referred to need not be 'real', but exist only in a universe of discourse. As an example, legal systems use vocabulary referring to 'legal persons' that are collective entities that have rights. One says the legal doctrine has an ontological commitment to non-singular individuals.
Pluralism is a term used in philosophy, referring to a worldview of multiplicity, often used in opposition to monism or dualism. The term has different meanings in metaphysics, ontology, epistemology and logic. In metaphysics, it is the view that there are in fact many different substances in nature that constitute reality. In ontology, pluralism refers to different ways, kinds, or modes of being. For example, a topic in ontological pluralism is the comparison of the modes of existence of things like 'humans' and 'cars' with things like 'numbers' and some other concepts as they are used in science.
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic.
Essence has various meanings and uses for different thinkers and in different contexts. It is used in philosophy and theology as a designation for the property or set of properties or attributes that make an entity the entity it is or, expressed negatively, without which it would lose its identity. Essence is contrasted with accident, which is a property or attribute the entity has accidentally or contingently, but upon which its identity does not depend.
Predicable is, in scholastic logic, a term applied to a classification of the possible relations in which a predicate may stand to its subject. It is not to be confused with 'praedicamenta', the scholastics' term for Aristotle's ten Categories.
The Categories is a text from Aristotle's Organon that enumerates all the possible kinds of things that can be the subject or the predicate of a proposition. They are "perhaps the single most heavily discussed of all Aristotelian notions". The work is brief enough to be divided not into books, as is usual with Aristotle's works, but into fifteen chapters.

Haecceity is a term from medieval scholastic philosophy, first coined by followers of Duns Scotus to denote a concept that he seems to have originated: the irreducible determination of a thing that makes it this particular thing. Haecceity is a person's or object's thisness, the individualising difference between the concept "a man" and the concept "Socrates". In modern philosophy of physics, it is sometimes referred to as primitive thisness.
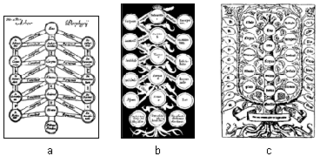
The Porphyrian tree or Tree of Porphyry is a classic device for illustrating a "scale of being", attributed to the 3rd century CE Greek neoplatonist philosopher and logician Porphyry, and revived through the translations of Boethius.
The Isagoge or "Introduction" to Aristotle's "Categories", written by Porphyry in Greek and translated into Latin by Boethius, was the standard textbook on logic for at least a millennium after his death. It was composed by Porphyry in Sicily during the years 268–270, and sent to Chrysaorium, according to all the ancient commentators Ammonius, Elias, and David. The work includes the highly influential hierarchical classification of genera and species from substance in general down to individuals, known as the Tree of Porphyry, and an introduction which mentions the problem of universals.
Philosophy of logic is the area of philosophy that studies the scope and nature of logic. It investigates the philosophical problems raised by logic, such as the presuppositions often implicitly at work in theories of logic and in their application. This involves questions about how logic is to be defined and how different logical systems are connected to each other. It includes the study of the nature of the fundamental concepts used by logic and the relation of logic to other disciplines. According to a common characterisation, philosophical logic is the part of the philosophy of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. But other theorists draw the distinction between the philosophy of logic and philosophical logic differently or not at all. Metalogic is closely related to the philosophy of logic as the discipline investigating the properties of formal logical systems, like consistency and completeness.
An ontological argument is a philosophical argument, made from an ontological basis, that is advanced in support of the existence of God. Such arguments tend to refer to the state of being or existing. More specifically, ontological arguments are commonly conceived a priori in regard to the organization of the universe, whereby, if such organizational structure is true, God must exist.

Predication in philosophy refers to an act of judgement where one term is subsumed under another. A comprehensive conceptualization describes it as the understanding of the relation expressed by a predicative structure primordially through the opposition between particular and general or the one and the many.
References
- ↑ King, Peter (1992). "Duns Scotus on the Common Nature and the Individual Differentia". Philosophical Topics. 20 (2): 51–76. ISSN 0276-2080 . Retrieved 4 February 2024.


