Geodesy or geodetics is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems. Geodesy is an earth science and many consider the study of Earth's shape and gravity to be central to that science. It is also a discipline of applied mathematics.
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic re the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates.
A geographic coordinate system (GCS) is a spherical or geodetic coordinate system for measuring and communicating positions directly on Earth as latitude and longitude. It is the simplest, oldest and most widely used of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.
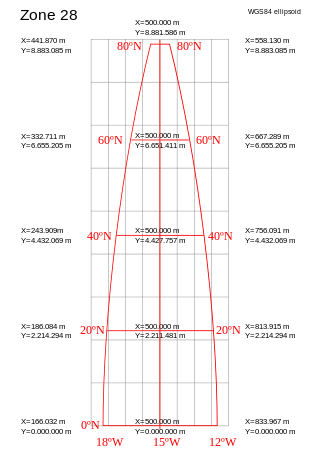
A projected coordinate system – also called a projected coordinate reference system, planar coordinate system, or grid reference system – is a type of spatial reference system that represents locations on Earth using Cartesian coordinates (x, y) on a planar surface created by a particular map projection. Each projected coordinate system, such as "Universal Transverse Mercator WGS 84 Zone 26N," is defined by a choice of map projection (with specific parameters), a choice of geodetic datum to bind the coordinate system to real locations on the earth, an origin point, and a choice of unit of measure. Hundreds of projected coordinate systems have been specified for various purposes in various regions.
The World Geodetic System (WGS) is a standard used in cartography, geodesy, and satellite navigation including GPS. The current version, WGS 84, defines an Earth-centered, Earth-fixed coordinate system and a geodetic datum, and also describes the associated Earth Gravitational Model (EGM) and World Magnetic Model (WMM). The standard is published and maintained by the United States National Geospatial-Intelligence Agency.
In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.
A geodetic datum or geodetic system is a global datum reference or reference frame for unambiguously representing the position of locations on Earth by means of either geodetic coordinates or geocentric coordinates. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a horizontal position, across the Earth's surface, in latitude and longitude or another related coordinate system. A vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). A three-dimensional datum enables the expression of both horizontal and vertical position components in a unified form. The concept can be generalized for other celestial bodies as in planetary datums.
The European Terrestrial Reference System 1989 (ETRS89) is an ECEF geodetic Cartesian reference frame, in which the Eurasian Plate as a whole is static. The coordinates and maps in Europe based on ETRS89 are not subject to change due to the continental drift.
A spatial reference system (SRS) or coordinate reference system (CRS) is a framework used to precisely measure locations on the surface of Earth as coordinates. It is thus the application of the abstract mathematics of coordinate systems and analytic geometry to geographic space. A particular SRS specification comprises a choice of Earth ellipsoid, horizontal datum, map projection, origin point, and unit of measure. Thousands of coordinate systems have been specified for use around the world or in specific regions and for various purposes, necessitating transformations between different SRS.
The North American Datum (NAD) is the horizontal datum now used to define the geodetic network in North America. A datum is a formal description of the shape of the Earth along with an "anchor" point for the coordinate system. In surveying, cartography, and land-use planning, two North American Datums are in use for making lateral or "horizontal" measurements: the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). Both are geodetic reference systems based on slightly different assumptions and measurements.
Local tangent plane coordinates (LTP) are part of a spatial reference system based on the tangent plane defined by the local vertical direction and the Earth's axis of rotation. They are also known as local ellipsoidal system, local geodetic coordinate system, local vertical, local horizontal coordinates (LVLH), or topocentric coordinates. It consists of three coordinates: one represents the position along the northern axis, one along the local eastern axis, and one represents the vertical position. Two right-handed variants exist: east, north, up (ENU) coordinates and north, east, down (NED) coordinates. They serve for representing state vectors that are commonly used in aviation and marine cybernetics.
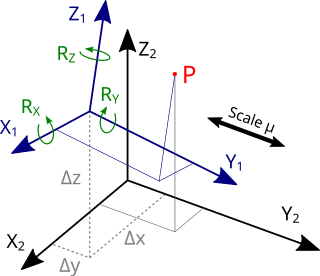
The Helmert transformation is a geometric transformation method within a three-dimensional space. It is frequently used in geodesy to produce datum transformations between datums. The Helmert transformation is also called a seven-parameter transformation and is a similarity transformation.
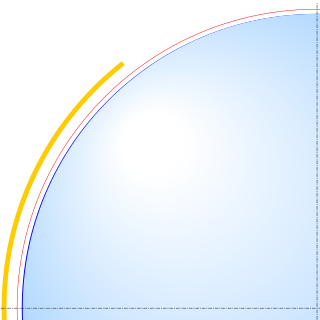
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.
Geodetic coordinates are a type of curvilinear orthogonal coordinate system used in geodesy based on a reference ellipsoid. They include geodetic latitude (north/south) ϕ, longitude (east/west) λ, and ellipsoidal heighth. The triad is also known as Earth ellipsoidal coordinates.
The Hellenic Geodetic Reference System 1987 or HGRS87 is a geodetic system commonly used in Greece (SRID=2100). The system specifies a local geodetic datum and a projection system. In some documents it is called Greek Geodetic Reference System 1987 or GGRS87.
The IERS Reference Meridian (IRM), also called the International Reference Meridian, is the prime meridian maintained by the International Earth Rotation and Reference Systems Service (IERS). It passes about 5.3 arcseconds east of George Biddell Airy's 1851 transit circle which is 102 metres (335 ft) at the latitude of the Royal Observatory, Greenwich. Thus it differs slightly from the historical Greenwich Meridian.
Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator or WGS 84/Pseudo-Mercator is a variant of the Mercator map projection and is the de facto standard for Web mapping applications. It rose to prominence when Google Maps adopted it in 2005. It is used by virtually all major online map providers, including Google Maps, CARTO, Mapbox, Bing Maps, OpenStreetMap, Mapquest, Esri, and many others. Its official EPSG identifier is EPSG:3857, although others have been used historically.
Well-known text representation of coordinate reference systems is a text markup language for representing spatial reference systems and transformations between spatial reference systems. The formats were originally defined by the Open Geospatial Consortium (OGC) and described in their Simple Feature Access and Well-known text representation of coordinate reference systems specifications. The current standard definition is ISO 19162:2019. This supersedes ISO 19162:2015.
A planetary coordinate system is a generalization of the geographic, geodetic, and the geocentric coordinate systems for planets other than Earth. Similar coordinate systems are defined for other solid celestial bodies, such as in the selenographic coordinates for the Moon. The coordinate systems for almost all of the solid bodies in the Solar System were established by Merton E. Davies of the Rand Corporation, including Mercury, Venus, Mars, the four Galilean moons of Jupiter, and Triton, the largest moon of Neptune. A planetary datum is a generalization of geodetic datums for other planetary bodies, such as the Mars datum; it requires the specification of physical reference points or surfaces with fixed coordinates, such as a specific crater for the reference meridian or the best-fitting equigeopotential as zero-level surface.
