
The exponential function is a mathematical function denoted by or . Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the operation of taking powers of a number, but various modern definitions allow it to be rigorously extended to all real arguments , including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to consider the exponential function to be "the most important function in mathematics".

Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, D. Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation.

Half-life is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive. The term is also used more generally to characterize any type of exponential decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life is doubling time.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

The reaction rate or rate of reaction is the speed at which a chemical reaction takes place, defined as proportional to the increase in the concentration of a product per unit time and to the decrease in the concentration of a reactant per unit time. Reaction rates can vary dramatically. For example, the oxidative rusting of iron under Earth's atmosphere is a slow reaction that can take many years, but the combustion of cellulose in a fire is a reaction that takes place in fractions of a second. For most reactions, the rate decreases as the reaction proceeds. A reaction's rate can be determined by measuring the changes in concentration over time.

A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and λ (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant:
Hemorheology, also spelled haemorheology, or blood rheology, is the study of flow properties of blood and its elements of plasma and cells. Proper tissue perfusion can occur only when blood's rheological properties are within certain levels. Alterations of these properties play significant roles in disease processes. Blood viscosity is determined by plasma viscosity, hematocrit and mechanical properties of red blood cells. Red blood cells have unique mechanical behavior, which can be discussed under the terms erythrocyte deformability and erythrocyte aggregation. Because of that, blood behaves as a non-Newtonian fluid. As such, the viscosity of blood varies with shear rate. Blood becomes less viscous at high shear rates like those experienced with increased flow such as during exercise or in peak-systole. Therefore, blood is a shear-thinning fluid. Contrarily, blood viscosity increases when shear rate goes down with increased vessel diameters or with low flow, such as downstream from an obstruction or in diastole. Blood viscosity also increases with increases in red cell aggregability.

In the context of radioactivity, activity or total activity (symbol A) is a physical quantity defined as the number of radioactive transformations per second that occur in a particular radionuclide. The unit of activity is the becquerel (symbol Bq), which is defined equivalent to reciprocal seconds (symbol s-1). The older, non-SI unit of activity is the curie (Ci), which is 3.7×1010 radioactive decay per second. Another unit of activity is the rutherford, which is defined as 1×106 radioactive decay per second.
In chemistry, the rate equation is an empirical differential mathematical expression for the reaction rate of a given reaction in terms of concentrations of chemical species and constant parameters only. For many reactions, the initial rate is given by a power law such as
In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium. Each relaxation process can be categorized by a relaxation time τ. The simplest theoretical description of relaxation as function of time t is an exponential law exp(−t/τ).
In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them. For an entire system to be at steady state, i.e. for all state variables of a system to be constant, there must be a flow through the system. A simple example of such a system is the case of a bathtub with the tap running but with the drain unplugged: after a certain time, the water flows in and out at the same rate, so the water level stabilizes and the system is in a steady state.
In pharmacology, clearance is a pharmacokinetic parameter representing the efficiency of drug elimination. This is the rate of elimination of a substance divided by its concentration. The parameter also indicates the theoretical volume of plasma from which a substance would be completely removed per unit time. Usually, clearance is measured in L/h or mL/min. The quantity reflects the rate of drug elimination divided by plasma concentration. Excretion, on the other hand, is a measurement of the amount of a substance removed from the body per unit time. While clearance and excretion of a substance are related, they are not the same thing. The concept of clearance was described by Thomas Addis, a graduate of the University of Edinburgh Medical School.
Standardized Kt/V, also std Kt/V, is a way of measuring (renal) dialysis adequacy. It was developed by Frank Gotch and is used in the United States to measure dialysis. Despite the name, it is quite different from Kt/V. In theory, both peritoneal dialysis and hemodialysis can be quantified with std Kt/V.
In science, e-folding is the time interval in which an exponentially growing quantity increases by a factor of e; it is the base-e analog of doubling time. This term is often used in many areas of science, such as in atmospheric chemistry, medicine and theoretical physics, especially when cosmic inflation is investigated. Physicists and chemists often talk about the e-folding time scale that is determined by the proper time in which the length of a patch of space or spacetime increases by the factor e mentioned above.
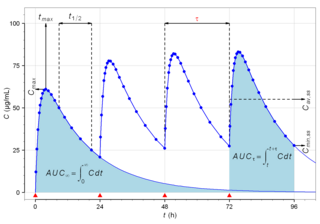
Biological half-life is the time taken for concentration of a biological substance to decrease from its maximum concentration (Cmax) to half of Cmax in the blood plasma. It is denoted by the abbreviation .

Dilution is the process of decreasing the concentration of a solute in a solution, usually simply by mixing with more solvent like adding more water to the solution. To dilute a solution means to add more solvent without the addition of more solute. The resulting solution is thoroughly mixed so as to ensure that all parts of the solution are identical.

Pharmacokinetics, sometimes abbreviated as PK, is a branch of pharmacology dedicated to describing how the body affects a specific substance after administration. The substances of interest include any chemical xenobiotic such as pharmaceutical drugs, pesticides, food additives, cosmetics, etc. It attempts to analyze chemical metabolism and to discover the fate of a chemical from the moment that it is administered up to the point at which it is completely eliminated from the body. Pharmacokinetics is based on mathematical modeling that places great emphasis on the relationship between drug plasma concentration and the time elapsed since the drug's administration. Pharmacokinetics is the study of how an organism affects the drug, whereas pharmacodynamics (PD) is the study of how the drug affects the organism. Both together influence dosing, benefit, and adverse effects, as seen in PK/PD models.
The plateau principle is a mathematical model or scientific law originally developed to explain the time course of drug action (pharmacokinetics). The principle has wide applicability in pharmacology, physiology, nutrition, biochemistry, and system dynamics. It applies whenever a drug or nutrient is infused or ingested at a relatively constant rate and when a constant fraction is eliminated during each time interval. Under these conditions, any change in the rate of infusion leads to an exponential increase or decrease until a new level is achieved. This behavior is also called an approach to steady state because rather than causing an indefinite increase or decrease, a natural balance is achieved when the rate of infusion or production is balanced by the rate of loss.

Entropy production is the amount of entropy which is produced during heat process to evaluate the efficiency of the process.
There is a strong scientific consensus that greenhouse effect due to carbon dioxide is a main driver of climate change. Following is an illustrative model meant for a pedagogical purpose, showing the main physical determinants of the effect.























