In propositional logic, affirming the consequent, sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency, is a formal fallacy of taking a true conditional statement under certain assumptions, and invalidly inferring its converse, even though that statement may not be true under the same assumptions. This arises when the consequent has other possible antecedents.
In propositional logic, modus ponens, also known as modus ponendo ponens, implication elimination, or affirming the antecedent, is a deductive argument form and rule of inference. It can be summarized as "P implies Q.P is true. Therefore, Q must also be true."
In propositional logic, modus tollens (MT), also known as modus tollendo tollens and denying the consequent, is a deductive argument form and a rule of inference. Modus tollens is a mixed hypothetical syllogism that takes the form of "If P, then Q. Not Q. Therefore, not P." It is an application of the general truth that if a statement is true, then so is its contrapositive. The form shows that inference from P implies Q to the negation of Q implies the negation of P is a valid argument.

A syllogism is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true.
Deductive reasoning is the process of drawing valid inferences. An inference is valid if its conclusion follows logically from its premises, meaning that it is impossible for the premises to be true and the conclusion to be false. For example, the inference from the premises "all men are mortal" and "Socrates is a man" to the conclusion "Socrates is mortal" is deductively valid. An argument is sound if it is valid and all its premises are true. One approach defines deduction in terms of the intentions of the author: they have to intend for the premises to offer deductive support to the conclusion. With the help of this modification, it is possible to distinguish valid from invalid deductive reasoning: it is invalid if the author's belief about the deductive support is false, but even invalid deductive reasoning is a form of deductive reasoning.
Denying the antecedent, sometimes also called inverse error or fallacy of the inverse, is a formal fallacy of inferring the inverse from an original statement. It is a type of mixed hypothetical syllogism in the form:
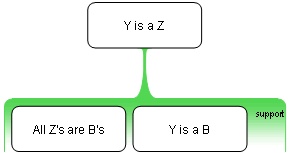
In classical logic, a hypothetical syllogism is a valid argument form, a deductive syllogism with a conditional statement for one or both of its premises. Ancient references point to the works of Theophrastus and Eudemus for the first investigation of this kind of syllogisms.
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly by his followers, the Peripatetics. It was revived after the third century CE by Porphyry's Isagoge.
Affirmative conclusion from a negative premise is a formal fallacy that is committed when a categorical syllogism has a positive conclusion and one or two negative premises.
The fallacy of four terms is the formal fallacy that occurs when a syllogism has four terms rather than the requisite three, rendering it invalid.
The existential fallacy, or existential instantiation, is a formal fallacy. In the existential fallacy, one presupposes that a class has members when one is not supposed to do so; i.e., when one should not assume existential import. Not to be confused with the 'Affirming the consequent', as in "If A, then B. B. Therefore A".
Illicit major is a formal fallacy committed in a categorical syllogism that is invalid because its major term is undistributed in the major premise but distributed in the conclusion.

Illicit minor is a formal fallacy committed in a categorical syllogism that is invalid because its minor term is undistributed in the minor premise but distributed in the conclusion.
The fallacy of exclusive premises is a syllogistic fallacy committed in a categorical syllogism that is invalid because both of its premises are negative.
In philosophical logic, the masked-man fallacy is committed when one makes an illicit use of Leibniz's law in an argument. Leibniz's law states that if A and B are the same object, then A and B are indiscernible. By modus tollens, this means that if one object has a certain property, while another object does not have the same property, the two objects cannot be identical. The fallacy is "epistemic" because it posits an immediate identity between a subject's knowledge of an object with the object itself, failing to recognize that Leibniz's Law is not capable of accounting for intensional contexts.
In logic and philosophy, a formal fallacy is a pattern of reasoning rendered invalid by a flaw in its logical structure that can neatly be expressed in a standard logic system, for example propositional logic. It is defined as a deductive argument that is invalid. The argument itself could have true premises, but still have a false conclusion. Thus, a formal fallacy is a fallacy in which deduction goes wrong, and is no longer a logical process. This may not affect the truth of the conclusion, since validity and truth are separate in formal logic.
A premise or premiss is a proposition—a true or false declarative statement—used in an argument to prove the truth of another proposition called the conclusion. Arguments consist of a set of premises and a conclusion.
The politician's syllogism, also known as the politician's logic or the politician's fallacy, is a logical fallacy of the form:
- We must do something.
- This is something.
- Therefore, we must do this.
Negative conclusion from affirmative premises is a syllogistic fallacy committed when a categorical syllogism has a negative conclusion yet both premises are affirmative. The inability of affirmative premises to reach a negative conclusion is usually cited as one of the basic rules of constructing a valid categorical syllogism.