Definition
The fallacious deduction is that: For every A, there is a B, such that C. Therefore, there is a B, such that for every A, C.
However, an inverse switching:
is logically valid.
A quantifier shift is a logical fallacy in which the quantifiers of a statement are erroneously transposed. The change in the logical nature of the statement may not be obvious when it is stated in a natural language like English.
The fallacious deduction is that: For every A, there is a B, such that C. Therefore, there is a B, such that for every A, C.
However, an inverse switching:
is logically valid.
1. Every person has a woman that is their mother. Therefore, there is a woman that is the mother of every person.
It is fallacious to conclude that there is one woman who is the mother of all people.
However, if the major premise ("every person has a woman that is their mother") is assumed to be true, then it is valid to conclude that there is some woman who is any given person's mother.
2. Everybody has something to believe in. Therefore, there is something that everybody believes in.
It is fallacious to conclude that there is some particular concept to which everyone subscribes.
It is valid to conclude that each person believes a given concept. But it is entirely possible that each person believes in a unique concept.
3. Every natural number has a successor , the smallest of all natural numbers that are greater than . Therefore, there is a natural number that is a successor to all natural numbers.
It is fallacious to conclude that there is a single natural number that is the successor of every natural number.
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.

The proof of Gödel's completeness theorem given by Kurt Gödel in his doctoral dissertation of 1929 is not easy to read today; it uses concepts and formalisms that are no longer used and terminology that is often obscure. The version given below attempts to represent all the steps in the proof and all the important ideas faithfully, while restating the proof in the modern language of mathematical logic. This outline should not be considered a rigorous proof of the theorem.

Saul Aaron Kripke is an American philosopher and logician in the analytic tradition. He is a Distinguished Professor of Philosophy at the Graduate Center of the City University of New York and emeritus professor at Princeton University. Since the 1960s, Kripke has been a central figure in a number of fields related to mathematical logic, modal logic, philosophy of language, philosophy of mathematics, metaphysics, epistemology, and recursion theory. Much of his work remains unpublished or exists only as tape recordings and privately circulated manuscripts.
In mathematical logic, a universal quantification is a type of quantifier, a logical constant which is interpreted as "given any" or "for all". It expresses that a predicate can be satisfied by every member of a domain of discourse. In other words, it is the predication of a property or relation to every member of the domain. It asserts that a predicate within the scope of a universal quantifier is true of every value of a predicate variable.
In the mathematical discipline of set theory, forcing is a technique for proving consistency and independence results. It was first used by Paul Cohen in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory.
Curry's paradox is a paradox in which an arbitrary claim F is proved from the mere existence of a sentence C that says of itself "If C, then F", requiring only a few apparently innocuous logical deduction rules. Since F is arbitrary, any logic having these rules allows one to prove everything. The paradox may be expressed in natural language and in various logics, including certain forms of set theory, lambda calculus, and combinatory logic.
Relevance logic, also called relevant logic, is a kind of non-classical logic requiring the antecedent and consequent of implications to be relevantly related. They may be viewed as a family of substructural or modal logics.
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.
Sequent calculus is, in essence, a style of formal logical argumentation where every line of a proof is a conditional tautology instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the style of natural deduction used by mathematicians than David Hilbert's earlier style of formal logic where every line was an unconditional tautology. There may be more subtle distinctions to be made; for example, there may be non-logical axioms upon which all propositions are implicitly dependent. Then sequents signify conditional theorems in a first-order language rather than conditional tautologies.
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason, the CoC and its variants have been the basis for Coq and other proof assistants.
The identity of indiscernibles is an ontological principle that states that there cannot be separate objects or entities that have all their properties in common. That is, entities x and y are identical if every predicate possessed by x is also possessed by y and vice versa; to suppose two things indiscernible is to suppose the same thing under two names. It states that no two distinct things can be exactly alike, but this is intended as a metaphysical principle rather than one of natural science. A related principle is the indiscernibility of identicals, discussed below.
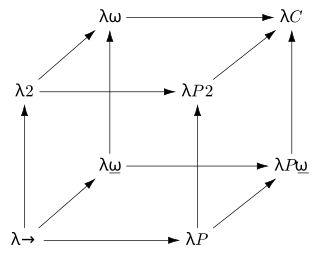
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke.
In modal logic, Sahlqvist formulas are a certain kind of modal formula with remarkable properties. The Sahlqvist correspondence theorem states that every Sahlqvist formula is canonical, and corresponds to a first-order definable class of Kripke frames.
In predicate logic, generalization is a valid inference rule. It states that if has been derived, then can be derived.
In logic, a rule of inference is admissible in a formal system if the set of theorems of the system does not change when that rule is added to the existing rules of the system. In other words, every formula that can be derived using that rule is already derivable without that rule, so, in a sense, it is redundant. The concept of an admissible rule was introduced by Paul Lorenzen (1955).
In logic, general frames are Kripke frames with an additional structure, which are used to model modal and intermediate logics. The general frame semantics combines the main virtues of Kripke semantics and algebraic semantics: it shares the transparent geometrical insight of the former, and robust completeness of the latter.

Markov's principle, named after Andrey Markov Jr, is a conditional existence statement for which there are many equivalent formulations, as discussed below.
In constructive mathematics, Church's thesis (CT) is an axiom stating that all total functions are computable. The axiom takes its name from the Church–Turing thesis, which states that every effectively calculable function is a computable function, but the constructivist version is much stronger, claiming that every function is computable.
In mathematical logic, the ancestral relation of a binary relation R is its transitive closure, however defined in a different way, see below.