
In mathematics, a Lie algebra is a vector space together with an operation called the Lie bracket, an alternating bilinear map , that satisfies the Jacobi identity. The Lie bracket of two vectors and is denoted . The vector space together with this operation is a non-associative algebra, meaning that the Lie bracket is not necessarily associative.

In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360°. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors.
In mathematics, the tensor product of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted
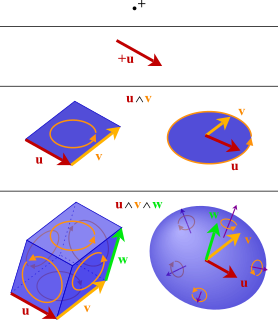
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors and , denoted by , is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of can be interpreted as the area of the parallelogram with sides and , which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning that for all vectors and , but, unlike the cross product, the exterior product is associative.
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since found applications in physics, Calabi–Yau manifolds, string theory, Chern–Simons theory, knot theory, Gromov–Witten invariants, topological quantum field theory, the Chern theorem etc.
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2‑grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions.

In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator. In the language of physics, one looks for a vector space together with a collection of operators on satisfying some fixed set of commutation relations, such as the relations satisfied by the angular momentum operators.
In mathematics, the universal enveloping algebra of a Lie algebra is the unital associative algebra whose representations correspond precisely to the representations of that Lie algebra.
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T•(V), is the algebra of tensors on V with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property.

In mathematics the spin group Spin(n) is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading.
In mathematics, the complexification of a vector space V over the field of real numbers yields a vector space VC over the complex number field, obtained by formally extending the scaling of vectors by real numbers to include their scaling ("multiplication") by complex numbers. Any basis for V may also serve as a basis for VC over the complex numbers.
The representation theory of groups is a part of mathematics which examines how groups act on given structures.
In mathematics, a graded vector space is a vector space that has the extra structure of a grading or a gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.
In mathematics, the Grothendieck group construction constructs an abelian group from a commutative monoid M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
In mathematics and theoretical physics, a supermatrix is a Z2-graded analog of an ordinary matrix. Specifically, a supermatrix is a 2×2 block matrix with entries in a superalgebra. The most important examples are those with entries in a commutative superalgebra or an ordinary field.
In mathematics, a real structure on a complex vector space is a way to decompose the complex vector space in the direct sum of two real vector spaces. The prototype of such a structure is the field of complex numbers itself, considered as a complex vector space over itself and with the conjugation map :{\mathbb {C} }\to {\mathbb {C} }\,} , with , giving the "canonical" real structure on , that is .
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics.
In algebra, the cofree coalgebra of a vector space or module is a coalgebra analog of the free algebra of a vector space. The cofree coalgebra of any vector space over a field exists, though it is more complicated than one might expect by analogy with the free algebra.





















































