Argumentation scheme

Last updated March 26, 2024

In argumentation theory, an argumentation scheme or argument scheme is a template that represents a common type of argument used in ordinary conversation. Many different argumentation schemes have been identified. Each one has a name (for example, argument from effect to cause) and presents a type of connection between premises and a conclusion in an argument, and this connection is expressed as a rule of inference. Argumentation schemes can include inferences based on different types of reasoning—deductive, inductive, abductive, probabilistic, etc.

Some basic features of argumentation schemes can be seen by examining the scheme called argument from effect to cause, which has the form: "If A occurs, then B will (or might) occur, and in this case B occurred, so in this case A presumably occurred."^[1]^: 170 This scheme may apply, for example, when someone argues: "Presumably there was a fire, since there was smoke and if there is a fire then there will be smoke." This example looks like the formal fallacy of affirming the consequent ("If A is true then B is also true, and B is true, so A must be true"), but in this example the material conditional logical connective ("A implies B") in the formal fallacy does not account for exactly why the semantic relation between premises and conclusion in the example, namely causality, may be reasonable ("fire causes smoke"), while not all formally valid conditional premises are reasonable (such as in the valid modus ponens argument "If there is a cat then there is smoke, and there is a cat, so there must be smoke"). As in this example, argumentation schemes typically recognize a variety of semantic (or substantive) relations that inference rules in classical logic ignore.^[2]^: 19 More than one argumentation scheme may apply to the same argument; in this example, the more complex abductive argumentation scheme may also apply.

Overview

Since the beginning of the discipline called rhetoric,^[3] the study of the types of argument has been a central issue.^[4]^[5]^[6] Knowledge of types of argument allows a speaker to find the argument form that is most suitable to a specific subject matter and situation. For example, arguments based on authority may be common in courts of law but not as frequent in a classroom discussion; arguments based on analogy are often effective in political discourse, but may be problematic in a scientific discussion.

The two interrelated goals of argument identification and analysis were the core of ancient dialectics (similar to debate), and specifically the branch called topics .^[7]^[8]^[9] In the 20th century, the ancient interest in types of arguments was revived in several academic disciplines, including education, artificial intelligence, legal philosophy, and discourse analysis.^[10]

The study of this ancient subject is mostly carried out today in the field of study called argumentation theory under the name of argumentation schemes.^[1]^[11]

An example of an argumentation scheme is the scheme for argument from position to know given below.^[12]^: 86

Argument from position to know
Premise:	a is in a position to know whether A is true or false.
Assertion premise:	a asserts that A is true ([or] false).
Conclusion:	A may plausibly be taken to be true ([or] false).

Following the usual convention in argumentation theory, arguments are given as a list of premises followed by a single conclusion . The premises are the grounds given by the speaker or writer for the hearer or reader to accept the conclusion as true or as provisionally true (regarded as true for now). An argumentation scheme's definition is not itself an argument, but represents the structure of an argument of a certain type. The letters in the scheme, lower case a and upper case A, need to be filled in if an argument is to be created from the scheme. Lower case a would be replaced by the name of a person and upper case A by a proposition, which might be true or false.

Argumentation theorist Douglas N. Walton gives the following example of an argument that fits the argument from position to know scheme: "It looks as if this passer-by knows the streets, and she says that City Hall is over that way; therefore, let's go ahead and accept the conclusion that City Hall is that way."^[12]^: 86

History

Among 20th-century authors, Chaïm Perelman and Lucie Olbrechts-Tyteca may have been the first to write at length about argumentation schemes, which they called argumentative schemes.^[13]^: 9^[14]^: 19 They present a long list of schemes together with explanation and examples in part three of The New Rhetoric (1958).^[13] The argumentation schemes in The New Rhetoric are not described in terms of their logical structure, as in more recent scholarship on argumentation schemes; instead they are given prose descriptions. The structure of the arguments is, nevertheless, considered important by the authors.^[13]^: 187

Perelman and Olbrechts-Tyteca also suggest a link between argumentation schemes and the loci (Latin) or topoi (Greek) of classical writers.^[13]^: 190 Both words, literally translated, mean "places" in their respective languages. Loci is a Latin translation of the Greek, topoi, used by Aristotle in his work, Topics , about logical argument and reasoning. Perelman and Olbrechts-Tyteca explain loci as: "headings under which arguments can be classified".^[13]^: 83 And they write, "They are associated with a concern to help a speaker's inventive efforts and involve the grouping of relevant material, so that it can be easily found again when required."^[13]^: 83 While Aristotle's treatment of topoi is not the same as the modern treatment of argumentation schemes, it is reasonable to consider Aristotle as the first writer in the genre.^[1]^: 267

The first contemporary writer to treat argumentation schemes in the way they are treated by current scholars and the way they are described in this article may have been Arthur Hastings in his 1962 Ph.D. dissertation.^[15]

Forms of inference

The study of argument in the field of argumentation theory since Perelman and Olbrechts-Tyteca's The New Rhetoric and Stephen Toulmin's The Uses of Argument,^[16] both first published in 1958, has been characterized by a recognition of the defeasible, non-monotonic nature of most ordinary everyday arguments and reasoning.^[14]^: 615 A defeasible argument is one that can be defeated, and that defeat is achieved when new information is discovered that shows that there was a relevant exception to an argument in the presence of which the conclusion can no longer be accepted. A common example used in textbooks concerns Tweety, a bird that may or may not fly:^[12]^: 72–73

(All) birds can fly;

Tweety is a bird;

Therefore, Tweety can fly.

The argument above (with the addition of "All", which is shown in parentheses) has the form of a logical syllogism and is, therefore, valid. If the first two statements, the premises, are true, then the third statement, the conclusion, must also be true. However, if we subsequently learn that Tweety is a penguin or has a broken wing, we can no longer conclude that Tweety can fly. In the context of deductive inference, we would have to conclude that our first premise was simply false. Deductive inference rules are not subject to exceptions. But there can be defeasible generalizations (defeasible inference rules). When we say that birds can fly, we mean that it is generally the case, subject to exceptions. We are justified in making the inference and accepting the conclusion that this particular bird can fly until we find out that an exception applies in this particular case.^[17]^: 21

In addition to deductive inference and defeasible inference, there is also probabilistic inference.^[12]^: 65–69 A probabilistic version of the generalization, "birds can fly", might be: "There is a 75% chance that a bird will be found to be able to fly" or "if something is a bird it probably can fly". The probabilistic version is also capable of being defeated (it is defeasible), but it includes the idea that the uncertainty might be quantifiable according to axioms of probability. (An exact number need not be attached as in the first example.^[12]^: 67)

In some theories, argumentation schemes are mostly schemes for argumentation with defeasible inference although there could be schemes for specialized areas of discourse using other forms of inference, such as probability in the sciences.^[1]^: 1–2 For most or all everyday arguments, the schemes are defeasible.^[18]

In other theories, the argumentation schemes are deductive or there is an attempt to interpret the schemes in a probabilistic way.^[19]

Examples

Argument from expert opinion

Argument from expert opinion can be considered a sub-type of the argument from position to know presented at the beginning of the article. In this case, the person who is in a position to know is an expert who knows about some field.^[20]

Argument from expert opinion^[20]
Major premise:	Source E is an expert in subject domain S containing proposition A.
Minor premise:	E asserts that proposition A is true (false).
Conclusion:	A is true (false).

Critical questions

The schemes of Walton (1996) and Walton, Reed & Macagno (2008) come with critical questions. Critical questions are questions that could be asked to throw doubt on the argument's support for its conclusion. They are targeted toward key assumptions that, if true, make the argument acceptable. The reason these assumptions are presented in the form of questions is that these schemes are a part of a dialectical theory of argumentation.^[1]^: 15 An argument is dialectical when it is a back and forth of argument and rebuttal or questioning. This can be the case even when there is only one reasoner, presenting arguments, then seeking out new information or sources of doubt, or critically probing their own initial assumptions. Since everyday arguments are typically defeasible, this is an approach to strengthening a case over time, testing each element of the case and discarding those parts that do not stand up to scrutiny.^[21]^: 47, 60 The critical questions for argument from expert opinion, given in Walton, Reed & Macagno (2008), are shown below.

Critical questions for argument from expert opinion^[20]
CQ1: Expertise question:	How credible is E as an expert source?
CQ2: Field question:	Is E an expert in the field that A is in?
CQ3: Opinion question:	What did E assert that implies A?
CQ4: Trustworthiness question:	Is E personally reliable as a source?
CQ5: Consistency question:	Is A consistent with what other experts assert?
CQ6: Backup evidence question:	Is E's assertion based on evidence?

Another version of the scheme argument from expert opinion, given in a textbook by Groarke, Tindale & Little (2013), does not include critical questions. Instead more of the key assumptions are included as additional premises of the argument.^[22]

Argument from ignorance

Argument from ignorance can be stated in a very informal way as, "if it were true, I would know it".^[17]^: 112 Walton gives the following example of an argument from ignorance: "The posted train schedule says that train 12 to Amsterdam stops at Haarlem and Amsterdam Central Station. We want to determine whether the train stops at Schipol. We can reason as follows: Since the schedule did not indicate that the train stops at Schipol, we can infer that it does not stop at Schipol."^[17]^: 112 Examples very much like this are well known in computer science discussions about the closed-world assumption for databases.^{[ citation needed ]} One can assume that the train operating authority has a policy of maintaining a complete database of all of the stops and of publishing accurate schedules. In such cases it is fairly well assured that the information on the published schedule is correct even though it is possible for information to be missing from the database or not included in some particular schedule posting.

The scheme and its accompanying critical questions are shown below.^[1]^: 327

Argument from ignorance^[20]
Major premise:	If A were true, then A would be known to be true.
Minor premise:	It is not the case that A is known to be true.
Conclusion:	Therefore, A is not true.

Critical questions for argument from ignorance^[20]
CQ1:	How far along has the search for evidence progressed?
CQ2:	Which side has the burden of proof in the dialogue as a whole? In other words, what is the ultimate probandum [claim that is to be proved] and who is supposed to prove it?
CQ3:	How strong does the proof need to be in order for this party to be successful in fulfilling the burden?

These critical questions, CQ2 and CQ3 especially, show the dialectical nature of the theory from which this scheme derives (that is, the scheme is based on a back and forth exchange between different parties). Two dialectical concerns are considered. It might be the case, as in some legal systems, that there is a presumption favoring a certain position—e.g., a presumption of innocence favoring the accused.^[1]^: 98 In that case, the burden of proof is on the accuser, and it would not be proper to argue in the opposite direction: "If the accused were innocent I would have known about it; I don't know about it; therefore, the accused is not innocent." Even if it were a proper argument, the standard of proof in such a case (as asked in CQ3) is very high, beyond a reasonable doubt, but the argument from ignorance alone might be very weak. When challenged, additional arguments would be needed to build a sufficiently strong case.^[1]^: 35

Other schemes

The following list is a selection of names of argumentation schemes from Walton, Reed & Macagno (2008); other sources may give different names:

Argument from witness testimony
Argument from popular opinion
Argument from popular practice
Argument from example
Argument from composition
Argument from division
Argument from oppositions
Argument from alternatives
Argument from verbal classification
Argument from definition to verbal classification
Argument from vagueness of a verbal classification
Argument from arbitrariness of a verbal classification
Argument from interaction of act and person
Argument from values
Argument from the group and its members
Practical reasoning argument
Argument from waste
Argument from sunk costs
Argument from correlation to cause
Argument from sign
Argument from evidence to a hypothesis
Argument from consequences
Argument from threat
Argument from fear appeal
Argument from danger appeal
Argument from need for help
Argument from distress
Argument from commitment
Ethotic argument
Generic ad hominem argument
Pragmatic inconsistency argument
Argument from inconsistent commitment
Circumstantial ad hominem argument
Argument from bias
Bias ad hominem argument
Argument from gradualism
Slippery slope argument

See Practical reason § In argumentation for a description of argumentation schemes for practical reasoning.

Relation to fallacies

Many of the names of argumentation schemes may be familiar because of their history as names of fallacies and because of the history of the teaching of fallacies in critical thinking and informal logic courses. In his groundbreaking work, Fallacies, C. L. Hamblin challenged the idea that the traditional fallacies are always fallacious.^[23]^[14]^: 25 Subsequently, Walton described the fallacies as kinds of arguments; they can be used properly and provide support for conclusions, support which is, however, provisional and the arguments defeasible. When used improperly they can be fallacious.^[24]

Uses

Argumentation schemes are used for argument identification, argument analysis, argument evaluation, and argument invention.^[25]

Argument identification

Argument identification is the identification of arguments in a text or spoken discourse. Many or most of the statements will not be arguments or parts of arguments. But some of those statements might look similar to arguments. Informal logicians have especially noted the similarity between words used to express arguments and those used to express explanations.^[26]^[27] Words like "because" or "since" can be used to introduce reasons that justify argumentative positions, but they can also be used to introduce explanations: e.g., "something is the way it is because of the following explanation". Schemes may aid in argument identification because they describe factors that distinguish the argument type from other text. For example, an argument from expert opinion refers to an expert and a field of expertise, both of which could be identified in a text. Some schemes contain more easily distinguished characteristics than others.

Argument mining

Argument mining is the automatic identification of arguments in natural language using computing technology.^[28] It also includes some of the tasks of argument analysis.^[28]^: 57 The same benefits from the use of argumentation schemes as described above for identification and analysis are relevant to argument mining. Linguistic features that distinguish specific schemes can be used by computer algorithms to identify instances of those schemes and therefore automatically identify the arguments that are of those kinds.^[28]^{: 109–113} Without the ability to notice such argumentative patterns, only features common to all arguments would be available. Feng & Hirst (2011) proposed using argumentation schemes to automatically help fill in missing (implicit) premises in arguments, and they experimented with detecting instances of such schemes.^[29] Similar work was done by Lawrence and Reed, and reported in 2016.^[30]

Argument analysis

Argument analysis is distinguishing the premises and conclusion of an argument and determining their relationships (such as whether they are linked or convergent—see Argument map § Key features for diagrams of such relationships), determining the form of inference, and making explicit any implicit premises or conclusions.^[12]^{: 138–171} (These are the tasks of analysis from a logical perspective. When discourse and rhetorical analyses are considered, there would be additional tasks.)

The logical analysis of arguments is especially made difficult by the presence of implicit elements.^[13]^: 177^[27]^: 208–9 Their being implicit means that they are not present in the text (or spoken discourse) as statements; nevertheless, they are understood by the reader or hearer because of nonverbal elements or because of shared background knowledge from the social, cultural, or other shared, context. The implicit elements are also elements that are needed to make the argument cogent. Arguments containing implicit elements are called enthymemes , which is a term that was used by Aristotle in his works about dialectical reasoning and argument.^[14]^: 18 If an argument appears to match a scheme but is missing some elements, the scheme could be used as a guide to determining what is implicit in the argument.^[1]^: 189^[29]^: 987 An additional challenge with regard to this task could be that some schemes are easy to confuse. In Perelman and Olbrechts-Tyteca's concept of argumentative scheme, different schemes could apply to the same argument depending on the interpretation of the argument or the argument could be described by multiple schemes.^[13]^: 187–88 Hansen and Walton also write that arguments may fit multiple schemes.^[31]

Argument evaluation

Argument evaluation is the determination of the goodness of the argument: determining how good the argument is and whether, or with what reservations, it ought to be accepted. As mentioned above, in schemes accompanied by critical questions, a measure of the goodness of the argument is whether the critical questions can be appropriately answered. In other schemes, as in the example of the versions of argument from expert opinion in Groarke, Tindale & Little (2013), only good arguments fit the scheme because the criteria for goodness are included as premises,^[32] so if any one of the premises is false, the conclusion should not be accepted.

Argument invention

Argument invention is making new arguments to suit the occasion. As mentioned above, Perelman and Olbrechts-Tyteca attribute that use to the loci and topoi of the classical argumentation theorists.^[13]^[14]^: 20 They form a catalog of argument types from which arguers may draw in constructing their arguments. With argumentation schemes described by their structure with single letter variables as placeholders, constructing such arguments is just a matter of filling in the placeholders. The arguer could use other words that convey the same meaning and embellish the argument in other ways.

Related Research Articles

A false dilemma, also referred to as false dichotomy or false binary, is an informal fallacy based on a premise that erroneously limits what options are available. The source of the fallacy lies not in an invalid form of inference but in a false premise. This premise has the form of a disjunctive claim: it asserts that one among a number of alternatives must be true. This disjunction is problematic because it oversimplifies the choice by excluding viable alternatives, presenting the viewer with only two absolute choices when in fact, there could be many.

In classical rhetoric and logic, begging the question or assuming the conclusion is an informal fallacy that occurs when an argument's premises assume the truth of the conclusion. Historically, begging the question refers to a fault in a dialectical argument in which the speaker assumes some premise that has not been demonstrated to be true. In modern usage, it has come to refer to an argument in which the premises assume the conclusion without supporting it. This makes it more or less synonymous with circular reasoning.

A syllogism is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true.

A fallacy is the use of invalid or otherwise faulty reasoning in the construction of an argument that may appear to be well-reasoned if unnoticed. The term was introduced in the Western intellectual tradition by the Aristotelian De Sophisticis Elenchis.

Deductive reasoning is the mental process of drawing deductive inferences. An inference is deductively valid if its conclusion follows logically from its premises, i.e. it is impossible for the premises to be true and the conclusion to be false.

Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word infer means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle. Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction.

An enthymeme is an argument with a hidden premise. Enthymemes are usually developed from premises that accord with the audience's view of the world and what is taken to be common sense. However, where the general premise of a syllogism is supposed to be true, making the subsequent deduction necessary, the general premise of an enthymeme is merely probable, which leads only to a tentative conclusion. Originally theorized by Aristotle, there are four types of enthymeme, at least two of which are described in Aristotle's work.

Logical reasoning is a mental activity that aims to arrive at a conclusion in a rigorous way. It happens in the form of inferences or arguments by starting from a set of premises and reasoning to a conclusion supported by these premises. The premises and the conclusion are propositions, i.e. true or false claims about what is the case. Together, they form an argument. Logical reasoning is norm-governed in the sense that it aims to formulate correct arguments that any rational person would find convincing. The main discipline studying logical reasoning is logic.

Argumentation theory is the interdisciplinary study of how conclusions can be supported or undermined by premises through logical reasoning. With historical origins in logic, dialectic, and rhetoric, argumentation theory includes the arts and sciences of civil debate, dialogue, conversation, and persuasion. It studies rules of inference, logic, and procedural rules in both artificial and real-world settings.

Inventio, one of the five canons of rhetoric, is the method used for the discovery of arguments in Western rhetoric and comes from the Latin word, meaning "invention" or "discovery". Inventio is the central, indispensable canon of rhetoric, and traditionally means a systematic search for arguments.

Informal fallacies are a type of incorrect argument in natural language. The source of the error is not just due to the form of the argument, as is the case for formal fallacies, but can also be due to their content and context. Fallacies, despite being incorrect, usually appear to be correct and thereby can seduce people into accepting and using them. These misleading appearances are often connected to various aspects of natural language, such as ambiguous or vague expressions, or the assumption of implicit premises instead of making them explicit.

In philosophy of logic, defeasible reasoning is a kind of provisional reasoning that is rationally compelling, though not deductively valid. It usually occurs when a rule is given, but there may be specific exceptions to the rule, or subclasses that are subject to a different rule. Defeasibility is found in literatures that are concerned with argument and the process of argument, or heuristic reasoning.

In logic and philosophy, a formal fallacy, deductive fallacy, logical fallacy or non sequitur is a pattern of reasoning rendered invalid by a flaw in its logical structure that can neatly be expressed in a standard logic system, for example propositional logic. It is defined as a deductive argument that is invalid. The argument itself could have true premises, but still have a false conclusion. Thus, a formal fallacy is a fallacy where deduction goes wrong, and is no longer a logical process. This may not affect the truth of the conclusion, since validity and truth are separate in formal logic.

Chaïm Perelman was a Belgian philosopher of Polish-Jewish origin. He was among the most important argumentation theorists of the twentieth century. His chief work is the Traité de l'argumentation – la nouvelle rhétorique (1958), with Lucie Olbrechts-Tyteca, translated into English as The New Rhetoric: A Treatise on Argumentation, by John Wilkinson and Purcell Weaver (1969).

Douglas Neil Walton was a Canadian academic and author, known for his books and papers on argumentation, logical fallacies and informal logic. He was a Distinguished Research Fellow of the Centre for Research in Reasoning, Argumentation, and Rhetoric (CRRAR) at the University of Windsor, Ontario, Canada, and before that (2008–2014), he held the Assumption Chair of Argumentation Studies at the University of Windsor. Walton's work has been used to better prepare legal arguments and to help develop artificial intelligence.

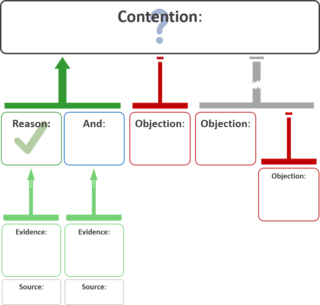
An argument map or argument diagram is a visual representation of the structure of an argument. An argument map typically includes all the key components of the argument, traditionally called the conclusion and the premises, also called contention and reasons. Argument maps can also show co-premises, objections, counterarguments, rebuttals, and lemmas. There are different styles of argument map but they are often functionally equivalent and represent an argument's individual claims and the relationships between them.

An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persuasion.

Informal logic encompasses the principles of logic and logical thought outside of a formal setting. However, the precise definition of "informal logic" is a matter of some dispute. Ralph H. Johnson and J. Anthony Blair define informal logic as "a branch of logic whose task is to develop non-formal standards, criteria, procedures for the analysis, interpretation, evaluation, criticism and construction of argumentation." This definition reflects what had been implicit in their practice and what others were doing in their informal logic texts.

Plausible reasoning is a method of deriving new conclusions from given known premises, a method different from the classical syllogistic argumentation methods of Aristotelian two-valued logic. The syllogistic style of argumentation is illustrated by the oft-quoted argument "All men are mortal, Socrates is a man, and therefore, Socrates is mortal." In contrast, consider the statement "if it is raining then it is cloudy." The only logical inference that one can draw from this is that "if it is not cloudy then it is not raining." But ordinary people in their everyday lives would conclude that "if it is not raining then being cloudy is less plausible," or "if it is cloudy then rain is more plausible." The unstated and unconsciously applied reasoning, arguably incorrect, that made people come to their conclusions is typical of plausible reasoning.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or logical truths. It studies how conclusions follow from premises due to the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. It examines arguments expressed in natural language while formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

References

1 2 3 4 5 6 7 8 9 Walton, Douglas N.; Reed, Chris; Macagno, Fabrizio (2008). Argumentation schemes . Cambridge; New York: Cambridge University Press. doi:10.1017/CBO9780511802034. ISBN 9780521897907. OCLC 181424052.
↑ Eemeren, Frans H. van, ed. (2001). Crucial concepts in argumentation theory. Amsterdam: Amsterdam University Press. ISBN 905356523X. OCLC 49333598.
↑ Braet, Antoine C. (March 2005). "The common topic in Aristotle's Rhetoric: precursor of the argumentation scheme". Argumentation. 19 (1): 65–83. doi:10.1007/s10503-005-2313-x. S2CID 145642868. See also: Aristotle (1991) [4th century BCE]. On rhetoric: a theory of civic discourse. Translated by Kennedy, George A. Oxford; New York: Oxford University Press. ISBN 9780195064865. OCLC 22629945.
↑ van Eemeren, Frans H.; Grootendorst, Rob (1992). Argumentation, communication, and fallacies: a pragma-dialectical perspective. Hillsdale: Lawrence Erlbaum Associates. ISBN 9780805810691. OCLC 24792772.
↑ Toulmin, Stephen; Rieke, Richard D.; Janik, Allan (1984) [1979]. An introduction to reasoning. New York: Macmillan Publishing Company. ISBN 9780024211606. OCLC 9783951.
↑ Kienpointner, Manfred (1992). Alltagslogik: Struktur und Funktion von Argumentationsmustern. Problemata (in German). Vol. 126. Stuttgart: Fromman-Holzboog. ISBN 9783772814624. OCLC 28724121.
↑ Aristotle (1997) [4th century BCE]. Topics. Clarendon Aristotle series. Translated by Smith, Robin. Oxford; New York: Clarendon Press; Oxford University Press. ISBN 9780198239420. OCLC 34411586.
↑ Boethius (1978) [522–23 BCE]. Boethius's De topicis differentiis . Translated by Stump, Eleonore. Ithaca: Cornell University Press. ISBN 9780801410673. OCLC 3414358.
↑ Cicero, Marcus Tullius (2003) [44 BCE]. Topica. Oxford classical monographs. Translated by Reinhardt, Tobias. Oxford; New York: Oxford University Press. ISBN 9780199263462. OCLC 54071435.
↑ Eemeren, Frans H. van; Grootendorst, Rob; Snoeck Henkemans, A. Francisca; et al. (1996). Fundamentals of argumentation theory: a handbook of historical backgrounds and contemporary developments . Mahwah, NJ: Lawrence Erlbaum Associates. ISBN 9780805818611. OCLC 33970847. It draws its data, assumptions, and methods from disciplines as disparate as formal logic and discourse analysis, linguistics and forensic science, philosophy and psychology, political science and education, sociology and law, and rhetoric and artificial intelligence.
↑ Rigotti, Eddo; Greco Morasso, Sara (2019). Inference in argumentation: a topics-based approach to argument schemes. Argumentation library. Vol. 34. Cham: Springer. doi:10.1007/978-3-030-04568-5. ISBN 9783030045661. OCLC 1096259194. S2CID 125412473.
1 2 3 4 5 6 Walton, Douglas N. (2006). Fundamentals of critical argumentation. Critical reasoning and argumentation. Cambridge, UK; New York: Cambridge University Press. doi:10.1017/CBO9780511807039. ISBN 0521823196. OCLC 57434163.
1 2 3 4 5 6 7 8 9 Perelman, Chaïm; Olbrechts-Tyteca, Lucie (1969) [1958]. The new rhetoric: a treatise on argumentation . Notre Dame, IN: University of Notre Dame Press. OCLC 21425.
1 2 3 4 5 Eemeren, Frans H. van; Garssen, Bart; Krabbe, Erik C. W.; Snoeck Henkemans, A. Francisca; Verheij, Bart; Wagemans, Jean H. M. (2014). Handbook of argumentation theory (Revised ed.). New York: Springer. doi:10.1007/978-90-481-9473-5. ISBN 9789048194728. OCLC 871004444.
↑ Walton, Reed & Macagno 2008 , p. 3; Hastings, Arthur Claude (August 1962). A reformulation of the modes of reasoning in argumentation (Ph.D. thesis). Evanston, IL: Northwestern University. OCLC 18518112. ProQuest 288066554. For extensive review of the history, see also Walton, Reed & Macagno 2008, chapter 8 and section 7.3 for information about Hastings' treatment of argumentation schemes.
↑ Toulmin, Stephen (2003) [1958]. The uses of argument (Updated ed.). Cambridge, UK; New York: Cambridge University Press. doi:10.1017/CBO9780511840005. ISBN 0521827485. OCLC 51607421.
1 2 3 Walton, Douglas N. (1996). Argumentation schemes for presumptive reasoning. Mahwah, NJ: Lawrence Erlbaum Associates. ISBN 9780805820713. OCLC 32704843.
↑ Walton, Douglas N. (2004). "Defeasible modus ponens arguments". Abductive reasoning. Tuscaloosa: University of Alabama Press. p. 122. ISBN 0817314415. OCLC 55044871.
↑ For deductive and probabilistic, see secions 2.1 and 5 in: Lumer, Christoph (May 2011). "Argument schemes—an epistemological approach". In Zenker, Frank (ed.). Argumentation: cognition & community: 9th biennial conference of the Ontario Society for the Study of Argumentation, May 18–21, 2011, University of Windsor. OSSA 9. Windsor: Ontario Society for the Study of Argumentation. pp. 1–32. ISBN 9780920233665. OCLC 843227451. For another probabilistic approach, see section 6 in: Hahn, Ulrike; Oaksford, Mike; Harris, Adam J. L. (2013). "Testimony and argument: a Bayesian perspective". In Zenker, Frank (ed.). Bayesian argumentation: the practical side of probability. Synthese library. Vol. 362. Dordrecht: Springer. pp. 15–38. doi:10.1007/978-94-007-5357-0_2. ISBN 9789400753563. OCLC 826657415. And: Hahn, Ulrike; Hornikx, Jos (June 2016). "A normative framework for argument quality: argumentation schemes with a Bayesian foundation". Synthese . 193 (6): 1833–1873. doi:10.1007/s11229-015-0815-0. hdl: 2066/160400 . S2CID 255062152.
1 2 3 4 5 Tables from Walton, Reed & Macagno 2008 , p. 310.
↑ Rescher, Nicholas (1977). Dialectics: a controversy-oriented approach to the theory of knowledge . Albany: State University of New York Press. ISBN 087395372X. OCLC 3034395.
↑ Groarke, Leo; Tindale, Christopher W.; Little, J. Frederick (2013) [1997]. Good reasoning matters!: a constructive approach to critical thinking (5th ed.). Don Mills, Ont.; Oxford: Oxford University Press. ISBN 9780195445756. OCLC 799130281.
↑ See chapter 1 in: Hamblin, Charles Leonard (1993) [1970]. Fallacies. Studies in critical thinking and informal logic. Vol. 1. Newport News, VA: Vale Press. ISBN 9780916475246. OCLC 29690976.
↑ Bench-Capon, Trevor; Atkinson, Katie (2010). "Argumentation schemes: from informal logic to computational models" (PDF). In Reed, Chris; Tindale, Christopher W. (eds.). Dialectics, dialogue and argumentation: an examination of Douglas Walton's theories of reasoning and argument. Tributes. Vol. 12. London: College Publications. pp. 103–114. ISBN 9781848900059. OCLC 648095461.
↑ Janjua, Naeem Khalid (2014). "Argumentation life cycle". A defeasible logic programming-based framework to support argumentation in semantic web applications. Springer theses. Cham; New York: Springer. p. 33. doi:10.1007/978-3-319-03949-7. hdl:20.500.11937/2073. ISBN 9783319039480. OCLC 895194510.
↑ Hansen, Hans V.; Walton, Douglas N. (January 2013). "Argument kinds and argument roles in the Ontario provincial election, 2011". Journal of Argumentation in Context. 2 (2): 226–258. doi:10.1075/jaic.2.2.03han. SSRN 2334864. Section 6.5.
1 2 Walton, Douglas N. (March 2019). "Argumentation schemes & their application in argument mining". In Blair, J. Anthony (ed.). Studies in critical thinking. Windsor Studies in Argumentation. Vol. 8. Windsor: Centre for Research in Reasoning, Argumentation and Rhetoric, University of Windsor. pp. 177–211. doi: 10.22329/wsia.08.2019 . ISBN 9780920233863. OCLC 1125160111.
1 2 3 Stede, Manfred; Schneider, Jodi (2018). Argumentation mining. Synthesis lectures on human language technologies. Vol. 40. San Rafael, CA: Morgan & Claypool. pp. 1–191. doi:10.2200/S00883ED1V01Y201811HLT040. ISBN 9781681734590. OCLC 1083530996.
1 2 Feng, Vanessa Wei; Hirst, Graeme (June 2011). "Classifying arguments by scheme" (PDF). Proceedings of the 49th annual meeting of the Association for Computational Linguistics: human language technologies, 19 June 2011, Portland, Oregon, USA. ACL HLT. Stroudsburg, PA: Association for Computational Linguistics. pp. 987–996. ISBN 9781932432879. OCLC 1150262180.
↑ Lawrence, John; Reed, Chris (September 2016). "Argument mining using argumentation scheme structures" (PDF). In Baroni, Pietro; Gordon, Thomas F.; Scheffler, Tatjana; Stede, Manfred (eds.). Computational models of argument: proceedings of COMMA 2016. Frontiers in artificial intelligence and applications. Vol. 287. Amsterdam: IOS Press. pp. 379–390. doi:10.3233/978-1-61499-686-6-379. ISBN 9781614996859. OCLC 957551747. S2CID 29571966.
↑ Hansen & Walton 2013, section 7.3.
↑ Hansen, Hans V. (2019). Argument scheme theory. Third European conference on argumentation (ECA), June 24–June 27, 2019, Rijksuniversiteit Groningen, The Netherlands: proceedings.