A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a nucleus of a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
A breakwater is a permanent structure constructed at a coastal area to protect against tides, currents, waves, and storm surges. Breakwaters have been built since antiquity to protect anchorages, helping isolate vessels from marine hazards such as wind-driven waves. A breakwater, also known in some contexts as a jetty or a mole, may be connected to land or freestanding, and may contain a walkway or road for vehicle access.
A revetment in stream restoration, river engineering or coastal engineering is a facing of impact-resistant material applied to a bank or wall in order to absorb the energy of incoming water and protect it from erosion. River or coastal revetments are usually built to preserve the existing uses of the shoreline and to protect the slope.
In geophysics and reflection seismology, amplitude versus offset (AVO) or amplitude variation with offset is the general term for referring to the dependency of the seismic attribute, amplitude, with the distance between the source and receiver. AVO analysis is a technique that geophysicists can execute on seismic data to determine a rock's fluid content, porosity, density or seismic velocity, shear wave information, fluid indicators.
Riprap, also known as rip rap, rip-rap, shot rock, rock armour or rubble, is human-placed rock or other material used to protect shoreline structures against scour and water, wave, or ice erosion. Riprap is used to armor shorelines, streambeds, bridge abutments, foundational infrastructure supports and other shoreline structures against erosion. Common rock types used include granite and modular concrete blocks. Rubble from building and paving demolition is sometimes used, as well as specifically designed structures called tetrapods or similar concrete blocks. Riprap is also used underwater to cap immersed tubes sunken on the seabed to be joined into an undersea tunnel.
Accropode blocks are wave-dissipating concrete blocks designed to resist the action of waves on breakwaters and coastal structures.
An Xbloc is a wave-dissipating concrete block designed to protect shores, harbour walls, seawalls, breakwaters and other coastal structures from the direct impact of incoming waves. The Xbloc model was designed and developed in 2001 by the Dutch firm Delta Marine Consultants, now called BAM Infraconsult, a subsidiary of the Royal BAM Group. Xbloc has been subjected to extensive research by several universities.
In geophysics and reflection seismology, the Zoeppritz equations are a set of equations that describe the partitioning of seismic wave energy at an interface, due to mode conversion. They are named after their author, the German geophysicist Karl Bernhard Zoeppritz, who died before they were published in 1919.
The Benjamin–Bona–Mahony equation is the partial differential equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
Derrick's theorem is an argument by physicist G. H. Derrick which shows that stationary localized solutions to a nonlinear wave equation or nonlinear Klein–Gordon equation in spatial dimensions three and higher are unstable.
The Izbash formula is a mathematical expression used to calculate the stability of armourstone in flowing water environments.
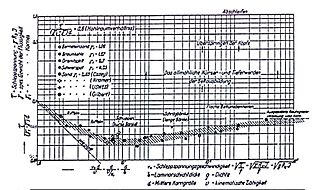
The Shields formula is a formula for the stability calculation of granular material in running water.
Armourstone is a generic term for broken stone with stone masses between 100 and 10,000 kilograms that is suitable for use in hydraulic engineering. Dimensions and characteristics for armourstone are laid down in European Standard EN13383. In the United States, there are a number of different standards and publications setting out different methodologies for classifying armourstone, ranging from weight-based classifications to gradation curves and size-based classifications.
The Van der Meer formula is a formula for calculating the required stone weight for armourstone under the influence of (wind) waves. This is necessary for the design of breakwaters and shoreline protection. Around 1985 it was found that the Hudson formula in use at that time had considerable limitations. That is why the Dutch government agency Rijkswaterstaat commissioned Deltares to start research for a more complete formula. This research, conducted by Jentsje van der Meer, resulted in the Van der Meer formula in 1988, as described in his dissertation. This formula reads
Ramón Iribarren CavanillesIng.D was a Spanish civil engineer and professor of ports at the School of Civil Engineering in Madrid. He was chairman of the Spanish delegation to the Permanent International Association of Navigation Congresses (PIANC) and was elected as an academic at the Spanish Royal Academy of Sciences, although he did not take up the latter position. He made notable contributions in the field of coastal engineering, including methods for the calculation of breakwater stability and research which led to the development of the Iribarren number.
Wave overtopping is the time-averaged amount of water that is discharged per structure length by waves over a structure such as a breakwater, revetment or dike which has a crest height above still water level.
Krystian Walenty Pilarczyk is a hydraulic engineer whose contributions to civil and hydraulic engineering include the development and improvement of the Izbash formula, along with the Pilarczyk formula for the stability of block revetments. He is the author and editor of a number of academic papers and textbooks on coastal, river, and hydraulic engineering subjects.
