In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson's equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer Lane and Robert Emden. The equation reads
A breakwater is a permanent structure constructed at a coastal area to protect against tides, currents, waves, and storm surges. Part of a coastal management system, breakwaters are installed to minimize erosion, and to protect anchorages, helping isolate vessels within them from marine hazards such as prop washes and wind-driven waves. A breakwater, also known in some contexts as a jetty, may be connected to land or freestanding, and may contain a walkway or road for vehicle access.
A revetment in stream restoration, river engineering or coastal engineering is a facing of impact-resistant material applied to a bank or wall in order to absorb the energy of incoming water and protect it from erosion. River or coastal revetments are usually built to preserve the existing uses of the shoreline and to protect the slope.
In geophysics and reflection seismology, amplitude versus offset (AVO) or amplitude variation with offset is the general term for referring to the dependency of the seismic attribute, amplitude, with the distance between the source and receiver. AVO analysis is a technique that geophysicists can execute on seismic data to determine a rock's fluid content, porosity, density or seismic velocity, shear wave information, fluid indicators.
Riprap, also known as rip rap, rip-rap, shot rock, rock armour or rubble, is human-placed rock or other material used to protect shoreline structures against scour and water, wave, or ice erosion. Ripraps are used to armor shorelines, streambeds, bridge abutments, foundational infrastructure supports and other shoreline structures against erosion. Common rock types used include granite and modular concrete blocks. Rubble from building and paving demolition is sometimes used, as well as specifically designed structures called tetrapods.
Accropode blocks are wave-dissipating concrete blocks designed to resist the action of waves on breakwaters and coastal structures.
An Xbloc is a wave-dissipating concrete block designed to protect shores, harbour walls, seawalls, breakwaters and other coastal structures from the direct impact of incoming waves. The Xbloc model was designed and developed by the Dutch firm Delta Marine Consultants, now called BAM Infraconsult, a subsidiary of the Royal BAM Group in 2001 and has been subjected to extensive research by several universities.
Beach evolution occurs at the shoreline where sea, lake or river water is eroding the land. Beaches exist where sand accumulated from centuries-old, recurrent processes that erode rocky and sedimentary material into sand deposits. River deltas deposit silt from upriver, accreting at the river's outlet to extend lake or ocean shorelines. Catastrophic events such as tsunamis, hurricanes, and storm surges accelerate beach erosion.
The Benjamin–Bona–Mahony equation is the partial differential equation
In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
Derrick's theorem is an argument by physicist G. H. Derrick which shows that stationary localized solutions to a nonlinear wave equation or nonlinear Klein–Gordon equation in spatial dimensions three and higher are unstable.
Dynamic revetment, also known as a "cobble berm", uses gravel or cobble-sized rocks to mimic a natural cobble storm beach for the purpose of reducing wave energy and stopping or slowing coastal erosion. Unlike seawalls, dynamic revetment is designed to allow wave action to rearrange the stones into an equilibrium profile, disrupting wave action and dissipating wave energy as the cobbles move. This can reduce the wave reflection which often contributes to beach scouring.
The Izbash formula is a formula for the stability calculation of armourstone in running water.
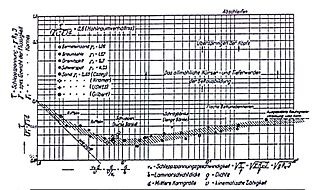
The Shields formula is a formula for the stability calculation of granular material in running water.
Armourstone is a generic term for broken stone with stone masses between 100 and 10,000 kilograms that is suitable for use in hydraulic engineering. Dimensions and characteristics are laid down in European Standard EN13383.
The Van der Meer formula is a formula for calculating the required stone weight for armourstone under the influence of (wind) waves. This is necessary for the design of breakwaters and shoreline protection. Around 1985 it was found that the Hudson formula in use at that time had considerable limitations. That is why the Dutch government agency Rijkswaterstaat commissioned Deltares to start research for a more complete formula. This research, conducted by Jentsje van der Meer, resulted in the Van der Meer formula in 1988, as described in his dissertation. This formula reads
