The anthropic principle, also known as the "observation selection effect", is the hypothesis, first proposed in 1957 by Robert Dicke, that the range of possible observations that we could make about the universe is limited by the fact that observations could only happen in a universe capable of developing intelligent life in the first place. Proponents of the anthropic principle argue that it explains why this universe has the age and the fundamental physical constants necessary to accommodate conscious life, since if either had been different, we would not have been around to make observations. Anthropic reasoning is often used to deal with the notion that the universe seems to be finely tuned for the existence of life.

Dice are small, throwable objects with marked sides that can rest in multiple positions. They are used for generating random values, commonly as part of tabletop games, including dice games, board games, role-playing games, and games of chance.

Frequentist probability or frequentism is an interpretation of probability; it defines an event's probability as the limit of its relative frequency in many trials. Probabilities can be found by a repeatable objective process. The continued use of frequentist methods in scientific inference, however, has been called into question.
The gambler's fallacy, also known as the Monte Carlo fallacy or the fallacy of the maturity of chances, is the incorrect belief that, if a particular event occurs more frequently than normal during the past, it is less likely to happen in the future, when it has otherwise been established that the probability of such events does not depend on what has happened in the past. Such events, having the quality of historical independence, are referred to as statistically independent. The fallacy is commonly associated with gambling, where it may be believed, for example, that the next dice roll is more than usually likely to be six because there have recently been fewer than the expected number of sixes.

In science, the probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. The more likely it is that the event will occur, the higher its probability. The probability of an impossible event is 0; that of an event that is certain to occur is 1. The probabilities of two complementary events A and B – either A occurs or B occurs – add up to 1. A simple example is the tossing of a fair (unbiased) coin. If a coin is fair, the two possible outcomes are equally likely; since these two outcomes are complementary and the probability of "heads" equals the probability of "tails", the probability of each of the two outcomes equals 1/2.

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.
Statistical regularity is a notion in statistics and probability theory that random events exhibit regularity when repeated enough times or that enough sufficiently similar random events exhibit regularity. It is an umbrella term that covers the law of large numbers, all central limit theorems and ergodic theorems.
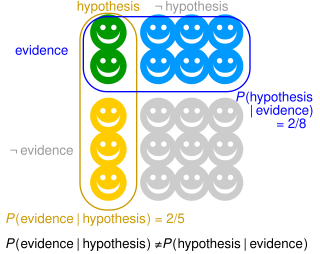
The prosecutor's fallacy is a fallacy of statistical reasoning involving a test for an occurrence, such as a DNA match. A positive result in the test may paradoxically be more likely to be an erroneous result than an actual occurrence, even if the test is very accurate. The fallacy is named because it is typically used by a prosecutor to exaggerate the probability of a criminal defendant's guilt. The fallacy can be used to support other claims as well – including the innocence of a defendant.
The representativeness heuristic is used when making judgments about the probability of an event under uncertainty. It is one of a group of heuristics proposed by psychologists Amos Tversky and Daniel Kahneman in the early 1970s as "the degree to which [an event] (i) is similar in essential characteristics to its parent population, and (ii) reflects the salient features of the process by which it is generated". Heuristics are described as "judgmental shortcuts that generally get us where we need to go – and quickly – but at the cost of occasionally sending us off course." Heuristics are useful because they use effort-reduction and simplification in decision-making.

The characterization of the universe as finely tuned suggests that the occurrence of life in the universe is very sensitive to the values of certain fundamental physical constants and that the observed values are, for some reason, improbable. If the values of any of certain free parameters in contemporary physical theories had differed only slightly from those observed, the evolution of the universe would have proceeded very differently and life as it is understood may not have been possible.
The Great Filter is one possible resolution of the Fermi paradox. It posits that in the development of life from the earliest stages of abiogenesis to reaching the highest levels of development on the Kardashev scale, there exists some particular barrier to development that makes detectable extraterrestrial life exceedingly rare.
The junkyard tornado, also known as Hoyle's fallacy, is an argument used to deride the probability of abiogenesis as comparable to "the chance that a tornado sweeping through a junkyard might assemble a Boeing 747." It was used originally by English astronomer Fred Hoyle (1915–2001), who applied statistical analysis to the origin of life, but similar observations predate Hoyle and have been found all the way back to Darwin's time, and indeed to Cicero in classical times. While Hoyle himself was an atheist, the argument has since become a mainstay in the rejection of evolution by religious groups.
Double counting is a fallacy in reasoning.

In common usage, randomness is the apparent or actual lack of pattern or predictability in information. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are, by definition, unpredictable, but if the probability distribution is known, the frequency of different outcomes over repeated events is predictable. For example, when throwing two dice, the outcome of any particular roll is unpredictable, but a sum of 7 will tend to occur twice as often as 4. In this view, randomness is not haphazardness; it is a measure of uncertainty of an outcome. Randomness applies to concepts of chance, probability, and information entropy.

In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is A and the event B is known or assumed to have occurred, "the conditional probability of A given B", or "the probability of A under the condition B", is usually written as P(A|B) or occasionally PB(A). This can also be understood as the fraction of probability B that intersects with A: .
Probability has a dual aspect: on the one hand the likelihood of hypotheses given the evidence for them, and on the other hand the behavior of stochastic processes such as the throwing of dice or coins. The study of the former is historically older in, for example, the law of evidence, while the mathematical treatment of dice began with the work of Cardano, Pascal, Fermat and Christiaan Huygens between the 16th and 17th century.
The "hot hand" is a phenomenon, previously considered a cognitive social bias, that a person who experiences a successful outcome has a greater chance of success in further attempts. The concept is often applied to sports and skill-based tasks in general and originates from basketball, where a shooter is more likely to score if their previous attempts were successful; i.e., while having the "hot hand.” While previous success at a task can indeed change the psychological attitude and subsequent success rate of a player, researchers for many years did not find evidence for a "hot hand" in practice, dismissing it as fallacious. However, later research questioned whether the belief is indeed a fallacy. Some recent studies using modern statistical analysis have observed evidence for the "hot hand" in some sporting activities; however, other recent studies have not observed evidence of the "hot hand". Moreover, evidence suggests that only a small subset of players may show a "hot hand" and, among those who do, the magnitude of the "hot hand" tends to be small.
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usually abbreviated as i.i.d., iid, or IID. IID was first defined in statistics and finds application in different fields such as data mining and signal processing.





