In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the Cartesian product of sets, the direct product of groups or rings, and the product of topological spaces. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.
In mathematics, a monoidal category is a category equipped with a bifunctor
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices.

In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group, the finite abelian groups, and the additive group of the integers, the real numbers, and every finite-dimensional vector space over the reals or a p-adic field.
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In functional programming, a monad is a structure that combines program fragments (functions) and wraps their return values in a type with additional computation. In addition to defining a wrapping monadic type, monads define two operators: one to wrap a value in the monad type, and another to compose together functions that output values of the monad type. General-purpose languages use monads to reduce boilerplate code needed for common operations. Functional languages use monads to turn complicated sequences of functions into succinct pipelines that abstract away control flow, and side-effects.
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite-dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in the 1930s by Richard Brauer and Cecil Nesbitt and were named after Georg Frobenius. Tadashi Nakayama discovered the beginnings of a rich duality theory, . Jean Dieudonné used this to characterize Frobenius algebras. Frobenius algebras were generalized to quasi-Frobenius rings, those Noetherian rings whose right regular representation is injective. In recent times, interest has been renewed in Frobenius algebras due to connections to topological quantum field theory.
In category theory, a branch of mathematics, Beck's monadicity theorem gives a criterion that characterises monadic functors, introduced by Jonathan Mock Beck in about 1964. It is often stated in dual form for comonads. It is sometimes called the Beck tripleability theorem because of the older term triple for a monad.
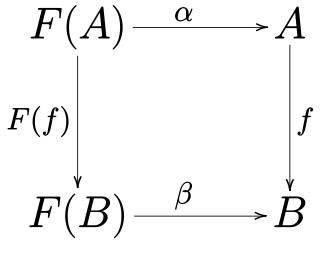
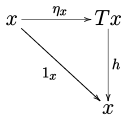
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, an operad is a structure that consists of abstract operations, each one having a fixed finite number of inputs (arguments) and one output, as well as a specification of how to compose these operations. Given an operad , one defines an algebra over to be a set together with concrete operations on this set which behave just like the abstract operations of . For instance, there is a Lie operad such that the algebras over are precisely the Lie algebras; in a sense abstractly encodes the operations that are common to all Lie algebras. An operad is to its algebras as a group is to its group representations.
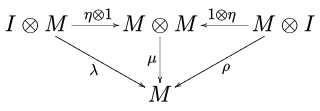
In category theory, a branch of mathematics, a monoid (or monoid object, or internal monoid, or algebra) (M, μ, η) in a monoidal category (C, ⊗, I) is an object M together with two morphisms
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the Eilenberg–Moore category. Kleisli categories are named for the mathematician Heinrich Kleisli.
In mathematics, a full subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector, or localization. Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.

In category theory, a strong monad over a monoidal category (C, ⊗, I) is a monad (T, η, μ) together with a natural transformation tA,B : A ⊗ TB → T(A ⊗ B), called (tensorial) strength, such that the diagrams
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
In category theory, a monoidal monad is a monad on a monoidal category such that the functor is a lax monoidal functor and the natural transformations and are monoidal natural transformations. In other words, is equipped with coherence maps and satisfying certain properties, and the unit and multiplication are monoidal natural transformations. By monoidality of , the morphisms and are necessarily equal.