U.S. Standard Atmosphere

Not to be confused with International Standard Atmosphere.

Comparison of the 1962 US Standard Atmosphere graph of geometric altitude against air density, pressure, the speed of sound and temperature with approximate altitudes of various objects.

The U.S. Standard Atmosphere is a static atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes or elevations. The model, based on an existing international standard, was first published in 1958 by the U.S. Committee on Extension to the Standard Atmosphere, and was updated in 1962, 1966, and 1976. It is largely consistent in methodology with the International Standard Atmosphere, differing mainly in the assumed temperature distribution at higher altitudes.

Visualization of composition by volume of Earth's atmosphere. Water vapor is not included, as this is highly variable. Each tiny cube (such as the one representing krypton) has one millionth of the volume of the entire block. Data is from NASA Langley.

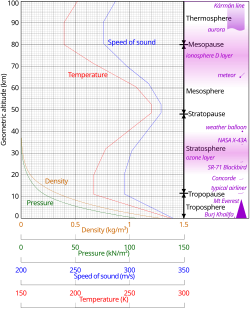
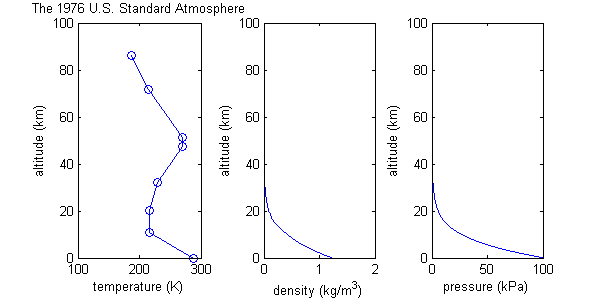
Methodology

The USSA mathematical model divides the atmosphere into layers with an assumed linear distribution of absolute temperature T against geopotential altitude h. ^[2] The other two values (pressure P and density ρ) are computed by simultaneously solving the equations resulting from:

• the vertical pressure variation, which relates pressure, density and geopotential altitude (using a standard pressure of 101,325 pascals (14.696 psi) at mean sea level as a boundary condition):

${\displaystyle {\frac {dP}{dh}}=-\rho g}$, and

• the ideal gas law in molar form, which relates pressure, density, and temperature:

${\displaystyle \ P=\rho R_{\rm {specific}}T}$

at each geopotential altitude, where g is the standard acceleration of gravity, and R_specific is the specific gas constant for dry air.

Air density must be calculated in order to solve for the pressure, and is used in calculating dynamic pressure for moving vehicles. Dynamic viscosity is an empirical function of temperature, and kinematic viscosity is calculated by dividing dynamic viscosity by the density.

Thus the standard consists of a tabulation of values at various altitudes, plus some formulas by which those values were derived.

To allow modeling conditions below mean sea level, the troposphere is actually extended to −2,000 feet (−610 m), where the temperature is 66.1 °F (18.9 °C), pressure is 15.79 pounds per square inch (108,900 Pa), and density is 0.08106 pounds per cubic foot (1.2985 kg/m³).

1962 version

The basic assumptions made for the 1962 version were: ^[3]

• air is a clean, dry, perfect gas mixture (c_p/c_v = 1.40)
• molecular weight to 90 km of 28.9644 (C-12 scale)
• principal sea-level constituents are assumed to be (in mole percent):
  • N₂ – 78.084%
  • O₂ – 20.9476%
  • Ar – 0.934%
  • CO₂ – 0.0314%
  • Ne – 0.001818%
  • He – 0.000524%
  • CH₄ – 0.0002%.
• assigned mean conditions at sea level are as follows :
  • P = 14.696 psi = 2116.22 psf = 101325 Pa = 760 mm Hg = 29.92  inHg = 0.1013250 MN/m²
  • T = 59 °F = 518.67 °R = 15 °C = 288.15 K
  • ρ = 0.0764734 lb/ft³ = 1.225 0 kg/m³
  • g = 32.174 1 ft/s² = 9.80665 m/s²
  • R^* = 1545.31 ft⋅lb/(lbmol⋅°R) = 8.31432 J/(mol⋅K).

The Federal Aviation Regulations define Standard Atmosphere in 14 CFR 1.1 by reference to the U.S. Standard Atmosphere, 1962 (Geopotential altitude tables).

1976 version

This is the most recent version and differs from previous versions only above 51 km:

Subscript b	Geopotential height above MSL [4]		Static pressure		Standard temperature (K)	Temperature lapse rate
	(m)	(ft)	(Pa)	(inHg)		(K/m)	(K/ft)
0	0	0	101325	29.92126	288.15	−0.0065	−0.001981
1	11,000	36,089	22632.1	6.683245	216.65	0.0	0.0
2	20,000	65,617	5474.89	1.616734	216.65	0.001	0.0003048
3	32,000	104,987	868.019	0.2563258	228.65	0.0028	0.0008534
4	47,000	154,199	110.906	0.0327506	270.65	0.0	0.0
5	51,000	167,323	66.9389	0.01976704	270.65	−0.0028	−0.0008534
6	71,000	232,940	3.95642	0.00116833	214.65	−0.002	−0.0006096
7	84,852	278,385			186.946

See also

• Atmospheric models
• NRLMSISE-00
• Barometric formula
• Standard temperature and pressure

References

1. Geometric altitude vs. temperature, pressure, density, and the speed of sound derived from the 1962 U.S. Standard Atmosphere.
2. Gyatt, Graham (2006-01-14): "The Standard Atmosphere". A mathematical model of the 1976 U.S. Standard Atmosphere.
3. Tuve, George Lewis; Bolz, Ray E. (1973). CRC handbook of tables for applied engineering science . Boca Raton: CRC Press. ISBN   0-8493-0252-8.
4. U.S. Standard Atmosphere, 1962, U.S. Government Printing Office, Washington, D.C., 1962, https://www.ngdc.noaa.gov/stp/space-weather/online-publications/miscellaneous/us-standard-atmosphere-1976/us-standard-atmosphere_st76-1562_noaa.pdf

Documents

• U.S. Extension to the ICAO Standard Atmosphere, U.S. Government Printing Office, Washington, D.C., 1958.
• U.S. Standard Atmosphere, 1962, U.S. Government Printing Office, Washington, D.C., 1962.
• U.S. Standard Atmosphere Supplements, 1966, U.S. Government Printing Office, Washington, D.C., 1966.
• U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976 (Linked file is 17 MB).

External links

• NASA GSFC ModelWeb
• A mathematical model of the 1976 U.S. Standard Atmosphere
• Online 1976 US Standard Atmosphere calculator and table generator
• Calculate 28 properties of 1976 Standard Atmosphere