In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability.
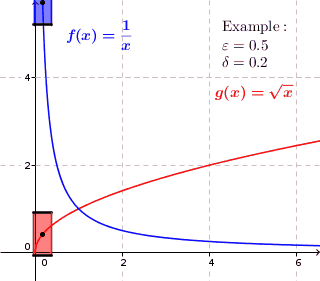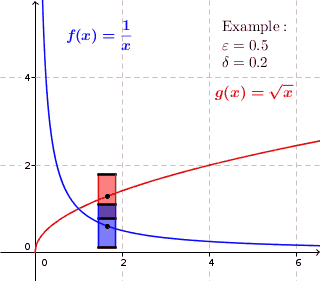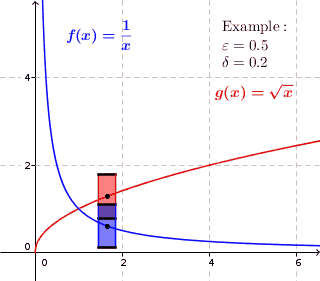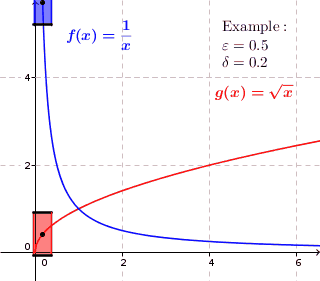
In mathematics, a real function of real numbers is said to be uniformly continuous if there is a positive real number such that function values over any function domain interval of the size are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number , then there is a positive real number such that at any and in any function interval of the size .
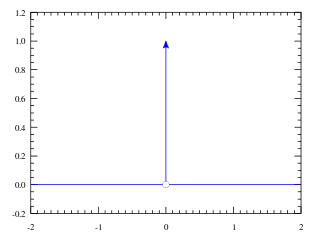
In mathematical physics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In the area of mathematics known as functional analysis, a reflexive space is a locally convex topological vector space (TVS) for which the canonical evaluation map from into its bidual is an isomorphism of TVSs. Since a normable TVS is reflexive if and only if it is semi-reflexive, every normed space is reflexive if and only if the canonical evaluation map from into its bidual is surjective; in this case the normed space is necessarily also a Banach space. In 1951, R. C. James discovered a Banach space, now known as James' space, that is not reflexive but is nevertheless isometrically isomorphic to its bidual.
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input.

Vapnik–Chervonenkis theory was developed during 1960–1990 by Vladimir Vapnik and Alexey Chervonenkis. The theory is a form of computational learning theory, which attempts to explain the learning process from a statistical point of view.
In functional analysis and operator theory, a bounded linear operator is a linear transformation between topological vector spaces (TVSs) and that maps bounded subsets of to bounded subsets of If and are normed vector spaces, then is bounded if and only if there exists some such that for all
The Arzelà–Ascoli theorem is a fundamental result of mathematical analysis giving necessary and sufficient conditions to decide whether every sequence of a given family of real-valued continuous functions defined on a closed and bounded interval has a uniformly convergent subsequence. The main condition is the equicontinuity of the family of functions. The theorem is the basis of many proofs in mathematics, including that of the Peano existence theorem in the theory of ordinary differential equations, Montel's theorem in complex analysis, and the Peter–Weyl theorem in harmonic analysis and various results concerning compactness of integral operators.

In mathematics, specifically functional analysis, a Banach space is said to have the approximation property (AP), if every compact operator is a limit of finite-rank operators. The converse is always true.
In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products, but for general Banach spaces or locally convex topological vector spaces the theory is notoriously subtle.
In geometric topology, Busemann functions are used to study the large-scale geometry of geodesics in Hadamard spaces and in particular Hadamard manifolds. They are named after Herbert Busemann, who introduced them; he gave an extensive treatment of the topic in his 1955 book "The geometry of geodesics".
In metric geometry, the metric envelope or tight span of a metric space M is an injective metric space into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes known as the injective envelope or hyperconvex hull of M. It has also been called the injective hull, but should not be confused with the injective hull of a module in algebra, a concept with a similar description relative to the category of R-modules rather than metric spaces.
In mathematics, Dvoretzky's theorem is an important structural theorem about normed vector spaces proved by Aryeh Dvoretzky in the early 1960s, answering a question of Alexander Grothendieck. In essence, it says that every sufficiently high-dimensional normed vector space will have low-dimensional subspaces that are approximately Euclidean. Equivalently, every high-dimensional bounded symmetric convex set has low-dimensional sections that are approximately ellipsoids.
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales.
In mathematics, the modulus of convexity and the characteristic of convexity are measures of "how convex" the unit ball in a Banach space is. In some sense, the modulus of convexity has the same relationship to the ε-δ definition of uniform convexity as the modulus of continuity does to the ε-δ definition of continuity.
In mathematics, a uniformly smooth space is a normed vector space satisfying the property that for every there exists such that if with and then















































