
In convex geometry, a convex set is a subset of an affine space that is closed under convex combinations. More specifically, in a Euclidean space, a convex region is a region where, for every pair of points within the region, every point on the straight line segment that joins the pair of points is also within the region. For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In linear algebra, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. The first usage of the concept of a vector space with an inner product is due to Peano, in 1898.
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis. A topological vector space is a vector space which is also a topological space, thereby admitting a notion of continuity. More specifically, its topological space has a uniform topological structure, allowing a notion of uniform convergence.
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the Lipschitz constant of the function. For instance, every function that has bounded first derivatives is Lipschitz.
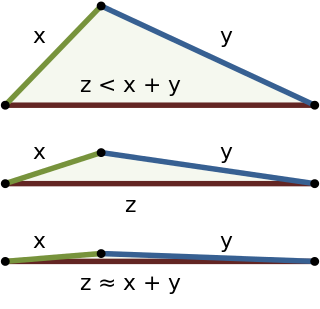
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If x, y, and z are the lengths of the sides of the triangle, with no side being greater than z, then the triangle inequality states that
In the area of mathematics known as functional analysis, a reflexive space is a Banach space that coincides with the continuous dual of its continuous dual space, both as linear space and as topological space. Reflexive Banach spaces are often characterized by their geometric properties.
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.
In functional analysis and related branches of mathematics, the Banach–Alaoglu theorem states that the closed unit ball of the dual space of a normed vector space is compact in the weak* topology. A common proof identifies the unit ball with the weak* topology as a closed subset of a product of compact sets with the product topology. As a consequence of Tychonoff's theorem, this product, and hence the unit ball within, is compact.
The Arzelà–Ascoli theorem is a fundamental result of mathematical analysis giving necessary and sufficient conditions to decide whether every sequence of a given family of real-valued continuous functions defined on a closed and bounded interval has a uniformly convergent subsequence. The main condition is the equicontinuity of the family of functions. The theorem is the basis of many proofs in mathematics, including that of the Peano existence theorem in the theory of ordinary differential equations, Montel's theorem in complex analysis, and the Peter–Weyl theorem in harmonic analysis.
In mathematical analysis, a modulus of continuity is a function ω : [0, ∞] → [0, ∞] used to measure quantitatively the uniform continuity of functions. So, a function f : I → R admits ω as a modulus of continuity if and only if
In linear algebra, functional analysis, and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to each vector in a vector space—except for the zero vector, which is assigned a length of zero. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.
In geometric topology, Busemann functions are used to study the large-scale geometry of geodesics in Hadamard spaces and in particular Hadamard manifolds. They are named after Herbert Busemann, who introduced them; he gave an extensive treatment of the topic in his 1955 book "The geometry of geodesics".
In mathematics, in the field of functional analysis, a Minkowski functional is a function that recovers a notion of distance on a linear space.

In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.
In functional analysis, the class of B-convex spaces is a class of Banach space. The concept of B-convexity was defined and used to characterize Banach spaces that have the strong law of large numbers by Anatole Beck in 1962; accordingly, "B-convexity" is understood as an abbreviation of Beck convexity. Beck proved the following theorem: A Banach space is B-convex if and only if every sequence of independent, symmetric, uniformly bounded and Radon random variables in that space satisfies the strong law of large numbers.
In mathematics, a uniformly smooth space is a normed vector space satisfying the property that for every there exists such that if with and then







