Closed graph theorem

This article is about closed graph theorems in general topology. For the closed graph theorem in functional analysis, see Closed graph theorem (functional analysis).

The graph of the cubic function ${\displaystyle f(x)=x^{3}-9x}$ on the interval ${\displaystyle [-4,4]}$ is closed because the function is continuous. The graph of the Heaviside function on ${\displaystyle [-2,2]}$ is not closed, because the function is not continuous.

In mathematics, the closed graph theorem may refer to one of several basic results characterizing continuous functions in terms of their graphs. Each gives conditions when functions with closed graphs are necessarily continuous.

Graphs and maps with closed graphs

Main article: Closed graph

If ${\displaystyle f:X\to Y}$ is a map between topological spaces then the graph of ${\displaystyle f}$ is the set ${\displaystyle \operatorname {Gr} f:=\{(x,f(x)):x\in X\}}$ or equivalently,

$${\displaystyle \operatorname {Gr} f:=\{(x,y)\in X\times Y:y=f(x)\}}$$

It is said that the graph of ${\displaystyle f}$ is closed if ${\displaystyle \operatorname {Gr} f}$ is a closed subset of ${\displaystyle X\times Y}$ (with the product topology).

Any continuous function into a Hausdorff space has a closed graph.

Any linear map, ${\displaystyle L:X\to Y,}$ between two topological vector spaces whose topologies are (Cauchy) complete with respect to translation invariant metrics, and if in addition (1a) ${\displaystyle L}$ is sequentially continuous in the sense of the product topology, then the map ${\displaystyle L}$ is continuous and its graph, Gr L, is necessarily closed. Conversely, if ${\displaystyle L}$ is such a linear map with, in place of (1a), the graph of ${\displaystyle L}$ is (1b) known to be closed in the Cartesian product space ${\displaystyle X\times Y}$, then ${\displaystyle L}$ is continuous and therefore necessarily sequentially continuous. ^[1]

Examples of continuous maps that do not have a closed graph

If ${\displaystyle X}$ is any space then the identity map ${\displaystyle \operatorname {Id} :X\to X}$ is continuous but its graph, which is the diagonal ${\displaystyle \operatorname {Gr} \operatorname {Id}$ :=\{(x,x):x\in X\},}, is closed in ${\displaystyle X\times X}$ if and only if ${\displaystyle X}$ is Hausdorff. ^[2] In particular, if ${\displaystyle X}$ is not Hausdorff then ${\displaystyle \operatorname {Id} :X\to X}$ is continuous but does not have a closed graph.

Let ${\displaystyle X}$ denote the real numbers ${\displaystyle \mathbb {R} }$ with the usual Euclidean topology and let ${\displaystyle Y}$ denote ${\displaystyle \mathbb {R} }$ with the indiscrete topology (where note that ${\displaystyle Y}$ is not Hausdorff and that every function valued in ${\displaystyle Y}$ is continuous). Let ${\displaystyle f:X\to Y}$ be defined by ${\displaystyle f(0)=1}$ and ${\displaystyle f(x)=0}$ for all ${\displaystyle x\neq 0}$. Then ${\displaystyle f:X\to Y}$ is continuous but its graph is not closed in ${\displaystyle X\times Y}$. ^[3]

Closed graph theorem in point-set topology

In point-set topology, the closed graph theorem states the following:

Closed graph theorem ^[4]  — If ${\displaystyle f:X\to Y}$ is a map from a topological space ${\displaystyle X}$ into a Hausdorff space ${\displaystyle Y,}$ then the graph of ${\displaystyle f}$ is closed if ${\displaystyle f:X\to Y}$ is continuous. The converse is true when ${\displaystyle Y}$ is compact. (Note that compactness and Hausdorffness do not imply each other.)

Proof

First part is essentially by definition.

Second part:

For any open ${\displaystyle V\subset Y}$ , we check ${\displaystyle f^{-1}(V)}$ is open. So take any ${\displaystyle x\in f^{-1}(V)}$ , we construct some open neighborhood ${\displaystyle U}$ of ${\displaystyle x}$ , such that ${\displaystyle f(U)\subset V}$ .

Since the graph of ${\displaystyle f}$ is closed, for every point ${\displaystyle (x,y')}$ on the "vertical line at x", with ${\displaystyle y'\neq f(x)}$ , draw an open rectangle ${\displaystyle U_{y'}\times V_{y'}}$ disjoint from the graph of ${\displaystyle f}$ . These open rectangles, when projected to the y-axis, cover the y-axis except at ${\displaystyle f(x)}$ , so add one more set ${\displaystyle V}$.

Naively attempting to take ${\displaystyle U:=\bigcap _{y'\neq f(x)}U_{y'}}$ would construct a set containing ${\displaystyle x}$, but it is not guaranteed to be open, so we use compactness here.

Since ${\displaystyle Y}$ is compact, we can take a finite open covering of ${\displaystyle Y}$ as ${\displaystyle \{V,V_{y'_{1}},...,V_{y'_{n}}\}}$.

Now take ${\displaystyle U:=\bigcap _{i=1}^{n}U_{y'_{i}}}$. It is an open neighborhood of ${\displaystyle x}$, since it is merely a finite intersection. We claim this is the open neighborhood of ${\displaystyle U}$ that we want.

Suppose not, then there is some unruly ${\displaystyle x'\in U}$ such that ${\displaystyle f(x')\not \in V}$ , then that would imply ${\displaystyle f(x')\in V_{y'_{i}}}$ for some ${\displaystyle i}$ by open covering, but then ${\displaystyle (x',f(x'))\in U\times V_{y'_{i}}\subset U_{y'_{i}}\times V_{y'_{i}}}$ , a contradiction since it is supposed to be disjoint from the graph of ${\displaystyle f}$ .

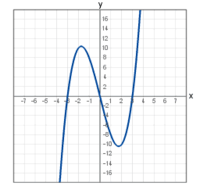
Non-Hausdorff spaces are rarely seen, but non-compact spaces are common. An example of non-compact ${\displaystyle Y}$ is the real line, which allows the discontinuous function with closed graph ${\displaystyle f(x)={\begin{cases}{\frac {1}{x}}{\text{ if }}x\neq 0,\\0{\text{ else}}\end{cases}}}$.

For set-valued functions

Closed graph theorem for set-valued functions ^[5]  — For a Hausdorff compact range space ${\displaystyle Y}$, a set-valued function ${\displaystyle F:X\to 2^{Y}}$ has a closed graph if and only if it is upper hemicontinuous and F(x) is a closed set for all ${\displaystyle x\in X}$.

In functional analysis

Main article: Closed graph theorem (functional analysis)

If ${\displaystyle T:X\to Y}$ is a linear operator between topological vector spaces (TVSs) then we say that ${\displaystyle T}$ is a closed operator if the graph of ${\displaystyle T}$ is closed in ${\displaystyle X\times Y}$ when ${\displaystyle X\times Y}$ is endowed with the product topology.

The closed graph theorem is an important result in functional analysis that guarantees that a closed linear operator is continuous under certain conditions. The original result has been generalized many times. A well known version of the closed graph theorems is the following.

Theorem ^{[6] [7]}  — A linear map between two F-spaces (e.g. Banach spaces) is continuous if and only if its graph is closed.

See also

• Almost open linear map
• Barrelled space  – Type of topological vector space
• Closed graph
• Closed linear operator
• Discontinuous linear map
• Kakutani fixed-point theorem  – On when a function f: S→Pow(S) on a compact nonempty convex subset S⊂ℝⁿ has a fixed point
• Open mapping theorem (functional analysis)  – Condition for a linear operator to be open
• Ursescu theorem  – Generalization of closed graph, open mapping, and uniform boundedness theorem
• Webbed space  – Space where open mapping and closed graph theorems hold
• Zariski's main theorem  – Theorem of algebraic geometry and commutative algebra

References

1. Rudin 1991, p. 51-52.
2. Rudin 1991, p. 50.
3. Narici & Beckenstein 2011, pp. 459–483.
4. Munkres 2000, pp. 163–172.
5. Aliprantis, Charlambos; Kim C. Border (1999). "Chapter 17". Infinite Dimensional Analysis: A Hitchhiker's Guide (3rd ed.). Springer.
6. Schaefer & Wolff 1999, p. 78.
7. Trèves (2006), p. 173

Bibliography

• Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN   3-540-13627-4. OCLC   17499190.
• Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN   978-0-471-80958-6
• Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN   978-3-519-02224-4. OCLC   8210342.
• Köthe, Gottfried (1983) [1969]. Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. Vol. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN   978-3-642-64988-2. MR   0248498. OCLC   840293704.
• Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN   978-0-13-181629-9. OCLC   42683260.
• Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN   978-1584888666. OCLC   144216834.
• Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN   978-0-07-054236-5. OCLC   21163277.
• Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN   978-1-4612-7155-0. OCLC   840278135.
• Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN   978-0-486-45352-1. OCLC   853623322.
• Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN   978-0-486-49353-4. OCLC   849801114.
• Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces . River Edge, N.J. London: World Scientific Publishing. ISBN   978-981-4488-15-0. MR   1921556. OCLC   285163112 – via Internet Archive.
• "Proof of closed graph theorem". PlanetMath .