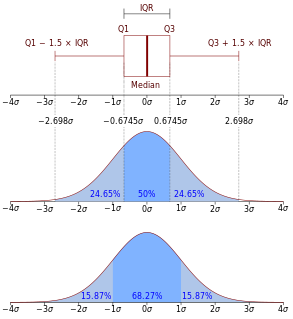
In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random and independent, and statistically identical over different time intervals of the same length. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
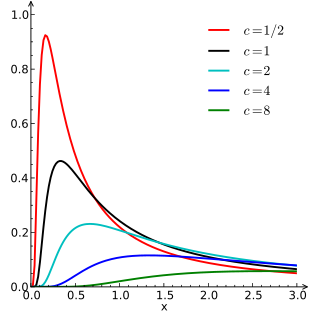
In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile. It is a special case of the inverse-gamma distribution. It is a stable distribution.

The scaled inverse chi-squared distribution is the distribution for x = 1/s2, where s2 is a sample mean of the squares of ν independent normal random variables that have mean 0 and inverse variance 1/σ2 = τ2. The distribution is therefore parametrised by the two quantities ν and τ2, referred to as the number of chi-squared degrees of freedom and the scaling parameter, respectively.

In probability theory, the inverse Gaussian distribution is a two-parameter family of continuous probability distributions with support on (0,∞).
The normal-inverse Gaussian distribution (NIG) is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the inverse Gaussian distribution. The NIG distribution was noted by Blaesild in 1977 as a subclass of the generalised hyperbolic distribution discovered by Ole Barndorff-Nielsen. In the next year Barndorff-Nielsen published the NIG in another paper. It was introduced in the mathematical finance literature in 1997.
The variance-gamma distribution, generalized Laplace distribution or Bessel function distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the gamma distribution. The tails of the distribution decrease more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The distribution was introduced in the financial literature by Madan and Seneta. The variance-gamma distributions form a subclass of the generalised hyperbolic distributions.
In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF). Every distribution possessing a moment-generating function is a member of a natural exponential family, and the use of such distributions simplifies the theory and computation of generalized linear models.
Financial models with long-tailed distributions and volatility clustering have been introduced to overcome problems with the realism of classical financial models. These classical models of financial time series typically assume homoskedasticity and normality cannot explain stylized phenomena such as skewness, heavy tails, and volatility clustering of the empirical asset returns in finance. In 1963, Benoit Mandelbrot first used the stable distribution to model the empirical distributions which have the skewness and heavy-tail property. Since -stable distributions have infinite -th moments for all , the tempered stable processes have been proposed for overcoming this limitation of the stable distribution.

In the theory of stochastic processes, a part of the mathematical theory of probability, the variance gamma process (VG), also known as Laplace motion, is a Lévy process determined by a random time change. The process has finite moments distinguishing it from many Lévy processes. There is no diffusion component in the VG process and it is thus a pure jump process. The increments are independent and follow a Variance-gamma distribution, which is a generalization of the Laplace distribution.
The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "version 1" and "version 2". However this is not a standard nomenclature.
In probability theory and statistics, the normal-Wishart distribution is a multivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a multivariate normal distribution with unknown mean and precision matrix.
In probability theory and statistics, the normal-inverse-Wishart distribution is a multivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a multivariate normal distribution with unknown mean and covariance matrix.