
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In analytical mechanics, generalized coordinates are a set of parameters used to represent the state of a system in a configuration space. These parameters must uniquely define the configuration of the system relative to a reference state. The generalized velocities are the time derivatives of the generalized coordinates of the system. The adjective "generalized" distinguishes these parameters from the traditional use of the term "coordinate" to refer to Cartesian coordinates.
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.
In statistics, the theory of minimum norm quadratic unbiased estimation (MINQUE) was developed by C. R. Rao. MINQUE is a theory alongside other estimation methods in estimation theory, such as the method of moments or maximum likelihood estimation. Similar to the theory of best linear unbiased estimation, MINQUE is specifically concerned with linear regression models. The method was originally conceived to estimate heteroscedastic error variance in multiple linear regression. MINQUE estimators also provide an alternative to maximum likelihood estimators or restricted maximum likelihood estimators for variance components in mixed effects models. MINQUE estimators are quadratic forms of the response variable and are used to estimate a linear function of the variances.
In statistics, the Vuong closeness test is a likelihood-ratio-based test for model selection using the Kullback–Leibler information criterion. This statistic makes probabilistic statements about two models. They can be nested, strictly non-nested or partially non-nested. The statistic tests the null hypothesis that the two models are equally close to the true data generating process, against the alternative that one model is closer. It cannot make any decision whether the "closer" model is the true model.
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power methods to find the "most useful" eigenvalues and eigenvectors of an Hermitian matrix, where is often but not necessarily much smaller than . Although computationally efficient in principle, the method as initially formulated was not useful, due to its numerical instability.
A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the states of the Markov process represents one of the phases.
In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester) or Lagrange−Sylvester interpolation expresses an analytic function f(A) of a matrix A as a polynomial in A, in terms of the eigenvalues and eigenvectors of A. It states that
In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF).
In probability and statistics, the class of exponential dispersion models (EDM), also called exponential dispersion family (EDF), is a set of probability distributions that represents a generalisation of the natural exponential family. Exponential dispersion models play an important role in statistical theory, in particular in generalized linear models because they have a special structure which enables deductions to be made about appropriate statistical inference.
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations.
Mechanics of planar particle motion is the analysis of the motion of particles gravitationally attracted to one another observed from non-inertial reference frames and the generalization of this problem to planetary motion. This type of analysis is closely related to centrifugal force, two-body problem, orbit and Kepler's laws of planetary motion. The mechanics of planar particle motion fall in the general field of analytical dynamics, and helps determine orbits from the given force laws. This article is focused more on the kinematic issues surrounding planar motion, which are the determination of the forces necessary to result in a certain trajectory given the particle trajectory.

In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, Mécanique analytique.

In probability theory and statistics, the generalized chi-squared distribution is the distribution of a quadratic form of a multinormal variable, or a linear combination of different normal variables and squares of normal variables. Equivalently, it is also a linear sum of independent noncentral chi-square variables and a normal variable. There are several other such generalizations for which the same term is sometimes used; some of them are special cases of the family discussed here, for example the gamma distribution.

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.
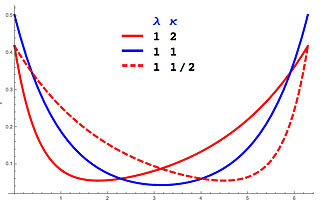
In probability theory and directional statistics, a wrapped asymmetric Laplace distribution is a wrapped probability distribution that results from the "wrapping" of the asymmetric Laplace distribution around the unit circle. For the symmetric case (asymmetry parameter κ = 1), the distribution becomes a wrapped Laplace distribution. The distribution of the ratio of two circular variates (Z) from two different wrapped exponential distributions will have a wrapped asymmetric Laplace distribution. These distributions find application in stochastic modelling of financial data.
The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. The quantum Fisher information of a state with respect to the observable is defined as





























































