
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

A random variable is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' can be misleading as its mathematical definition is not actually random nor a variable, but rather it is a function from possible outcomes in a sample space to a measurable space, often to the real numbers.
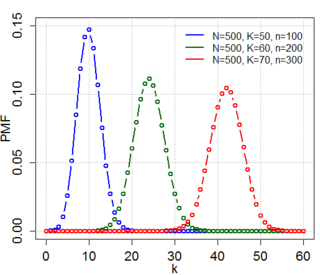
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.

In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time.

In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below.
Fisher's exact test is a statistical significance test used in the analysis of contingency tables. Although in practice it is employed when sample sizes are small, it is valid for all sample sizes. It is named after its inventor, Ronald Fisher, and is one of a class of exact tests, so called because the significance of the deviation from a null hypothesis can be calculated exactly, rather than relying on an approximation that becomes exact in the limit as the sample size grows to infinity, as with many statistical tests.

Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered for any given number of random variables. The joint distribution encodes the marginal distributions, i.e. the distributions of each of the individual random variables and the conditional probability distributions, which deal with how the outputs of one random variable are distributed when given information on the outputs of the other random variable(s).
In the field of information retrieval, divergence from randomness, one of the first models, is one type of probabilistic model. It is basically used to test the amount of information carried in the documents. It is based on Harter's 2-Poisson indexing-model. The 2-Poisson model has a hypothesis that the level of the documents is related to a set of documents which contains words occur relatively greater than the rest of the documents. It is not a 'model', but a framework for weighting terms using probabilistic methods, and it has a special relationship for term weighting based on notion of eliteness.
In mathematics, the Kolmogorov extension theorem is a theorem that guarantees that a suitably "consistent" collection of finite-dimensional distributions will define a stochastic process. It is credited to the English mathematician Percy John Daniell and the Russian mathematician Andrey Nikolaevich Kolmogorov.

In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of n trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data.

In probability theory and statistics, Wallenius' noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where items are sampled with bias.

In probability theory and statistics, Fisher's noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where sampling probabilities are modified by weight factors. It can also be defined as the conditional distribution of two or more binomially distributed variables dependent upon their fixed sum.
Subjective logic is a type of probabilistic logic that explicitly takes epistemic uncertainty and source trust into account. In general, subjective logic is suitable for modeling and analysing situations involving uncertainty and relatively unreliable sources. For example, it can be used for modeling and analysing trust networks and Bayesian networks.
In probability theory, the chain rule describes how to calculate the probability of the intersection of, not necessarily independent, events or the joint distribution of random variables respectively, using conditional probabilities. The rule is notably used in the context of discrete stochastic processes and in applications, e.g. the study of Bayesian networks, which describe a probability distribution in terms of conditional probabilities.
In statistics, a Pólya urn model, named after George Pólya, is a family of urn models that can be used to interpret many commonly used statistical models.
In probability theory, a beta negative binomial distribution is the probability distribution of a discrete random variable equal to the number of failures needed to get successes in a sequence of independent Bernoulli trials. The probability of success on each trial stays constant within any given experiment but varies across different experiments following a beta distribution. Thus the distribution is a compound probability distribution.
In mathematics, a statistical manifold is a Riemannian manifold, each of whose points is a probability distribution. Statistical manifolds provide a setting for the field of information geometry. The Fisher information metric provides a metric on these manifolds. Following this definition, the log-likelihood function is a differentiable map and the score is an inclusion.
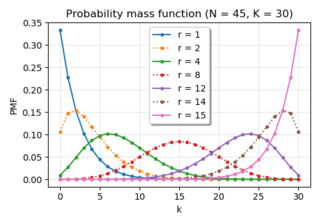
In probability theory and statistics, the negative hypergeometric distribution describes probabilities for when sampling from a finite population without replacement in which each sample can be classified into two mutually exclusive categories like Pass/Fail or Employed/Unemployed. As random selections are made from the population, each subsequent draw decreases the population causing the probability of success to change with each draw. Unlike the standard hypergeometric distribution, which describes the number of successes in a fixed sample size, in the negative hypergeometric distribution, samples are drawn until failures have been found, and the distribution describes the probability of finding successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of successes in a sample with exactly failures.
Bayesian hierarchical modelling is a statistical model written in multiple levels that estimates the parameters of the posterior distribution using the Bayesian method. The sub-models combine to form the hierarchical model, and Bayes' theorem is used to integrate them with the observed data and account for all the uncertainty that is present. The result of this integration is the posterior distribution, also known as the updated probability estimate, as additional evidence on the prior distribution is acquired.




















