
In mathematics, the arithmetic–geometric mean of two positive real numbers x and y is defined as follows:

In mathematics, a complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a symbol called the imaginary unit, and satisfying the equation i2 = −1. Because no real number satisfies this equation, i was called an imaginary number by René Descartes. For the complex number a + bi, a is called the real part and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number x:

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

Angular displacement of a body is the angle in radians, degrees or revolutions through which a point revolves around a centre or a specified axis in a specified sense. When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance, and orientation. Every non-trivial rotation is determined by its axis of rotation and its angle of rotation. Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map satisfies the definition of a rotation. Owing to the above properties, the set of all rotations is a group under composition. Rotations are not commutative, making it a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable; so it is in fact a Lie group. It is compact and has dimension 3.

In mathematics, a cube root of a number x is a number y such that y3 = x. All nonzero real numbers, have exactly one real cube root and a pair of complex conjugate cube roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8, denoted , is 2, because 23 = 8, while the other cube roots of 8 are and . The three cube roots of −27i are

In mathematics, the circle group, denoted by , is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

The dyadic transformation is the mapping

In probability theory and directional statistics, the von Mises distribution is a continuous probability distribution on the circle. It is a close approximation to the wrapped normal distribution, which is the circular analogue of the normal distribution. A freely diffusing angle on a circle is a wrapped normally distributed random variable with an unwrapped variance that grows linearly in time. On the other hand, the von Mises distribution is the stationary distribution of a drift and diffusion process on the circle in a harmonic potential, i.e. with a preferred orientation. The von Mises distribution is the maximum entropy distribution for circular data when the real and imaginary parts of the first circular moment are specified. The von Mises distribution is a special case of the von Mises–Fisher distribution on the N-dimensional sphere.

In mathematics, a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in are called double integrals, and integrals of a function of three variables over a region in are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

In mathematics, particularly in dynamical systems, Arnold tongues are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters. The regions of constant rotation number have been observed, for some dynamical systems, to form geometric shapes that resemble tongues, in which case they are called Arnold tongues.
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
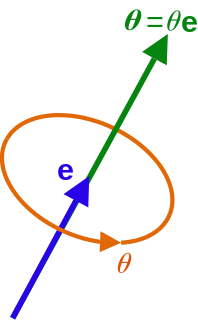
In mathematics, the axis–angle representation of a rotation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector e indicating the direction of an axis of rotation, and an angle θ describing the magnitude of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector e rooted at the origin because the magnitude of e is constrained. For example, the elevation and azimuth angles of e suffice to locate it in any particular Cartesian coordinate frame.
In algebra, casus irreducibilis is one of the cases that may arise in attempting to solve polynomials of degree 3 or higher with integer coefficients, to obtain roots that are expressed with radicals. It shows that many algebraic numbers are real-valued but cannot be expressed in radicals without introducing complex numbers. The most notable occurrence of casus irreducibilis is in the case of cubic polynomials that are irreducible over the rational numbers and have three real roots, which was proven by Pierre Wantzel in 1843. One can decide whether a given irreducible cubic polynomial is in casus irreducibilis using the discriminant Δ, via Cardano's formula. Let the cubic equation be given by
A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers.

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.























