Related Research Articles
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.
Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics — an area of study which supplements both theory and experiment.
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
James A. Yorke is a Distinguished University Research Professor of Mathematics and Physics and former chair of the Mathematics Department at the University of Maryland, College Park.
Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.
In lab experiments that study chaos theory, approaches designed to control chaos are based on certain observed system behaviors. Any chaotic attractor contains an infinite number of unstable, periodic orbits. Chaotic dynamics, then, consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different unstable, periodic orbit where it remains for a limited time and so forth. This results in a complicated and unpredictable wandering over longer periods of time.
Reservoir computing is a framework for computation derived from recurrent neural network theory that maps input signals into higher dimensional computational spaces through the dynamics of a fixed, non-linear system called a reservoir. After the input signal is fed into the reservoir, which is treated as a "black box," a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The first key benefit of this framework is that training is performed only at the readout stage, as the reservoir dynamics are fixed. The second is that the computational power of naturally available systems, both classical and quantum mechanical, can be used to reduce the effective computational cost.
Cybernetical physics is a scientific area on the border of cybernetics and physics which studies physical systems with cybernetical methods. Cybernetical methods are understood as methods developed within control theory, information theory, systems theory and related areas: control design, estimation, identification, optimization, pattern recognition, signal processing, image processing, etc. Physical systems are also understood in a broad sense; they may be either lifeless, living nature or of artificial (engineering) origin, and must have reasonably understood dynamics and models suitable for posing cybernetical problems. Research objectives in cybernetical physics are frequently formulated as analyses of a class of possible system state changes under external (controlling) actions of a certain class. An auxiliary goal is designing the controlling actions required to achieve a prespecified property change. Among typical control action classes are functions which are constant in time, functions which depend only on time, and functions whose value depends on measurement made at the same time or on previous instances. The last class is of special interest since these functions correspond to system analysis by means of external feedback.
In mathematics, the uncertainty exponent is a method of measuring the fractal dimension of a basin boundary. In a chaotic scattering system, the invariant set of the system is usually not directly accessible because it is non-attracting and typically of measure zero. Therefore, the only way to infer the presence of members and to measure the properties of the invariant set is through the basins of attraction. Note that in a scattering system, basins of attraction are not limit cycles therefore do not constitute members of the invariant set.
In geometry, exterior dimension is a type of dimension that can be used to characterize the scaling behavior of "fat fractals". A fat fractal is defined to be a subset of Euclidean space such that, for every point of the set and every sufficiently small number , the ball of radius centered at contains both a nonzero Lebesgue measure of points belonging to the fractal, and a nonzero Lebesgue measure of points that do not belong to the fractal. For such a set, the Hausdorff dimension is the same as that of the ambient space.
Miguel Angel Fernández Sanjuán is a Spanish Theoretical Physicist from Leon, Spain. He is known for his contributions in nonlinear dynamics, chaos theory, and control of chaos, and has published several scientific papers and popular news articles. He has supervised around 20 PhD students in Nonlinear Dynamics, Chaos and Complex Systems.
Guanrong Chen (陈关荣) or Ron Chen is a Chinese mathematician who made contributions to Chaos theory. He has been the chair professor and the founding director of the Centre for Chaos and Complex Networks at the City University of Hong Kong since 2000. Prior to that, he was a tenured full professor at the University of Houston, Texas. Chen was elected Member of the Academy of Europe in 2014, elected Fellow of The World Academy of Sciences in 2015, and elected IEEE Fellow in 1997. He is currently the editor-in-chief for the International Journal of Bifurcation and Chaos.
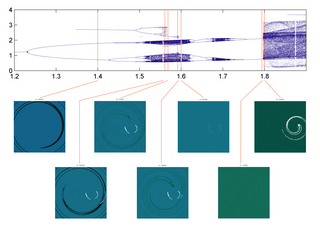
In applied mathematics and astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour.
Chaotic scattering is a branch of chaos theory dealing with scattering systems displaying a strong sensitivity to initial conditions. In a classical scattering system there will be one or more impact parameters, b, in which a particle is sent into the scatterer. This gives rise to one or more exit parameters, y, as the particle exits towards infinity. While the particle is traversing the system, there may also be a delay time, T—the time it takes for the particle to exit the system—in addition to the distance travelled, s. In certain systems the two will be equivalent—see below. In a chaotic scattering system, a minute change in the impact parameter, may give rise to a very large change in the exit parameters.
Edward Ott is an American physicist most noted for his contributions to the development of chaos theory.
Ying-Cheng Lai is a Chinese theoretical physicist/electrical engineer who works in the field of chaos theory and complex dynamical systems. He is among the pioneers in the field of relativistic quantum chaos. Currently, he works at Arizona State University as a Regents Professor. He also holds an ISS Chair Professorship in Electrical Engineering.
In mathematics, a strange nonchaotic attractor (SNA) is a form of attractor which, while converging to a limit, is strange, because it is not piecewise differentiable, and also non-chaotic, in that its Lyapunov exponents are non-positive. SNAs were introduced as a topic of study by Grebogi et al. in 1984. SNAs can be distinguished from periodic, quasiperiodic and chaotic attractors using the 0-1 test for chaos.
In the mathematics of chaotic dynamical systems, in the Pyragas method of stabilizing a periodic orbit, an appropriate continuous controlling signal is injected into the system, whose intensity is nearly zero as the system evolves close to the desired periodic orbit but increases when it drifts away from the desired orbit. Both the Pyragas and OGY methods are part of a general class of methods called "closed loop" or "feedback" methods which can be applied based on knowledge of the system obtained through solely observing the behavior of the system as a whole over a suitable period of time. The method was proposed by Lithuanian physicist Kęstutis Pyragas.
References
- ↑ "Web of Science Predicts 2016 Nobel Prize Winners". Thomson Reuters. September 21, 2016. Archived from the original on 2016-09-21. Retrieved 2016-09-30.
- ↑ "Professor Celso Grebogi FRSE - The Royal Society of Edinburgh". The Royal Society of Edinburgh. Retrieved 2018-06-26.
- Grebogi, Celso; Ott, Edward; Yorke, James A. (1987-10-30). "Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamics". Science. 238 (4827): 632–638. doi:10.1126/science.238.4827.632. ISSN 0036-8075.
- Ott, Edward; Grebogi, Celso; Yorke, James A. (1990-03-12). "Controlling chaos". Physical Review Letters. 64 (11): 1196–1199. doi:10.1103/PhysRevLett.64.1196. ISSN 0031-9007.
- Shinbrot, Troy; Grebogi, Celso; Yorke, James A.; Ott, Edward (1993). "Using small perturbations to control chaos". Nature. 363 (6428): 411–417. doi:10.1038/363411a0. ISSN 0028-0836.
- M. A. F. Sanjuán Recent progress in controlling chaos, World Scientific 2010
