Definitions
The outer billiards map
Let P be a convex shape in the plane. Given a point x0 outside P, there is typically a unique point x1 (also outside P) so that the line segment connecting x0 to x1 is tangent to P at its midpoint and a person walking from x0 to x1 would see P on the right. (See Figure.) The map F: x0 -> x1 is called the outer billiards map.
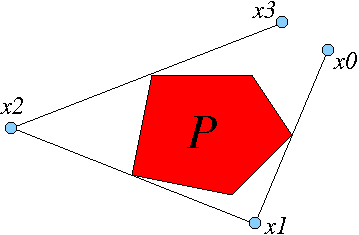
The inverse (or backwards) outer billiards map is also defined, as the map x1 -> x0. One gets the inverse map simply by replacing the word right by the word left in the definition given above. The figure shows the situation in the Euclidean plane, but the definition in the hyperbolic plane is essentially the same.
Orbits
An outer billiards orbit is the set of all iterations of the point, namely ... x0 ↔ x1 ↔ x2 ↔ x3 ... That is, start at x0 and iteratively apply both the outer billiards map and the backwards outer billiards map. When P is a strictly convex shape, such as an ellipse, every point in the exterior of P has a well defined orbit. When P is a polygon, some points might not have well-defined orbits, on account of the potential ambiguity of choosing the midpoint of the relevant tangent line. Nevertheless, in the polygonal case, almost every point has a well-defined orbit.
- An orbit is called periodic if it eventually repeats.
- An orbit is called aperiodic (or non-periodic) if it is not periodic.
- An orbit is called bounded (or stable) if some bounded region in the plane contains the whole orbit.
- An orbit is called unbounded (or unstable) if it is not bounded.
Higher-dimensional spaces
Defining an outer billiards system in a higher-dimensional space is beyond the scope of this article. Unlike the case of ordinary billiards, the definition is not straightforward. One natural setting for the map is a complex vector space. In this case, there is a natural choice of line tangent to a convex body at each point. One obtains these tangents by starting with the normals and using the complex structure to rotate 90 degrees. These distinguished tangent lines can be used to define the outer billiards map roughly as above. [1]

