Mayfield's Paradox states that to keep everyone out of an information system requires an infinite amount of money, and to get everyone onto an information system also requires infinite money, while costs between these extremes are relatively low. [1]
The paradox is depicted as a U-curve, where the cost of a system is on the vertical axis, and the percentage of humanity that can access the system is on the horizontal axis. Acceptance[ clarification needed ] of this paradox by the information security community was immediate[ when? ], because it was consistent with the professional experiences of this group. Mayfield's Paradox points out that, at some point of the curve, additional security becomes unrealistically expensive. Conversely, at some point of the curve, it becomes unrealistically expensive to add additional users.
Based on the Paradox the Menz brothers developed the "Menz Theorems of Information and Physical Security". The theorems present two formulas covering access and security of both information systems and physical facilities. They are used to help determine allocation of resources and response levels.
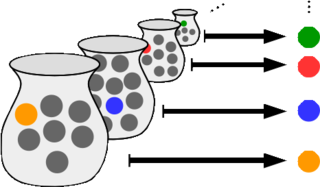
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by arbitrarily choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that Failed to parse : x_{i}\in S_{i} for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word ἀξίωμα (axíōma), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

The Einstein–Podolsky–Rosen (EPR) paradox is a thought experiment proposed by physicists Albert Einstein, Boris Podolsky and Nathan Rosen which argues that the description of physical reality provided by quantum mechanics is incomplete. In a 1935 paper titled "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?", they argued for the existence of "elements of reality" that were not part of quantum theory, and speculated that it should be possible to construct a theory containing these hidden variables. Resolutions of the paradox have important implications for the interpretation of quantum mechanics.
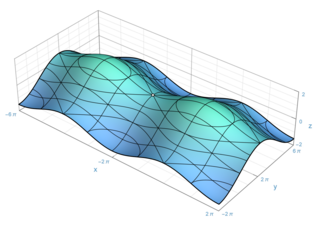
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

Time travel is the hypothetical activity of traveling into the past or future. Time travel is a widely recognized concept in philosophy and fiction, particularly science fiction. In fiction, time travel is typically achieved through the use of a hypothetical device known as a time machine. The idea of a time machine was popularized by H. G. Wells' 1895 novel The Time Machine.
The Novikov self-consistency principle, also known as the Novikov self-consistency conjecture and Larry Niven's law of conservation of history, is a principle developed by Russian physicist Igor Dmitriyevich Novikov in the mid-1980s. Novikov intended it to solve the problem of paradoxes in time travel, which is theoretically permitted in certain solutions of general relativity that contain what are known as closed timelike curves. The principle asserts that if an event exists that would cause a paradox or any "change" to the past whatsoever, then the probability of that event is zero. It would thus be impossible to create time paradoxes.
Arrow's impossibility theorem, the general possibility theorem or Arrow's paradox is an impossibility theorem in social choice theory that states that when voters have three or more distinct alternatives (options), no ranked voting electoral system can convert the ranked preferences of individuals into a community-wide ranking while also meeting the specified set of criteria: unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem is often cited in discussions of voting theory as it is further interpreted by the Gibbard–Satterthwaite theorem. The theorem is named after economist and Nobel laureate Kenneth Arrow, who demonstrated the theorem in his doctoral thesis and popularized it in his 1951 book Social Choice and Individual Values. The original paper was titled "A Difficulty in the Concept of Social Welfare".
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van Stockum in 1937 and later confirmed by Kurt Gödel in 1949, who discovered a solution to the equations of general relativity (GR) allowing CTCs known as the Gödel metric; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity which would replace GR, an idea which Stephen Hawking labeled the chronology protection conjecture. Others note that if every closed timelike curve in a given space-time passes through an event horizon, a property which can be called chronological censorship, then that space-time with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.
The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts a gravitational singularity in black hole formation. The Hawking singularity theorem is based on the Penrose theorem and it is interpreted as a gravitational singularity in the Big Bang situation. Penrose was awarded the Nobel Prize in Physics in 2020 "for the discovery that black hole formation is a robust prediction of the general theory of relativity", which he shared with Reinhard Genzel and Andrea Ghez.

A Gabriel's horn is a type of geometric figure that has infinite surface area but finite volume. The name refers to the Christian tradition where the archangel Gabriel blows the horn to announce Judgment Day. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli in the 17th century.

In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved.

In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. This theorem is related to the rusty compass equivalence.

A physical paradox is an apparent contradiction in physical descriptions of the universe. While many physical paradoxes have accepted resolutions, others defy resolution and may indicate flaws in theory. In physics as in all of science, contradictions and paradoxes are generally assumed to be artifacts of error and incompleteness because reality is assumed to be completely consistent, although this is itself a philosophical assumption. When, as in fields such as quantum physics and relativity theory, existing assumptions about reality have been shown to break down, this has usually been dealt with by changing our understanding of reality to a new one which remains self-consistent in the presence of the new evidence.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted E2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in three-dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them without changing their shape. However, the pieces themselves are not "solids" in the usual sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces.

In mathematics, Cramer's paradox or the Cramer–Euler paradox is the statement that the number of points of intersection of two higher-order curves in the plane can be greater than the number of arbitrary points that are usually needed to define one such curve. It is named after the Genevan mathematician Gabriel Cramer.
The Fei–Ranis model of economic growth is a dualism model in developmental economics or welfare economics that has been developed by John C. H. Fei and Gustav Ranis and can be understood as an extension of the Lewis model. It is also known as the Surplus Labor model. It recognizes the presence of a dual economy comprising both the modern and the primitive sector and takes the economic situation of unemployment and underemployment of resources into account, unlike many other growth models that consider underdeveloped countries to be homogenous in nature. According to this theory, the primitive sector consists of the existing agricultural sector in the economy, and the modern sector is the rapidly emerging but small industrial sector. Both the sectors co-exist in the economy, wherein lies the crux of the development problem. Development can be brought about only by a complete shift in the focal point of progress from the agricultural to the industrial economy, such that there is augmentation of industrial output. This is done by transfer of labor from the agricultural sector to the industrial one, showing that underdeveloped countries do not suffer from constraints of labor supply. At the same time, growth in the agricultural sector must not be negligible and its output should be sufficient to support the whole economy with food and raw materials. Like in the Harrod–Domar model, saving and investment become the driving forces when it comes to economic development of underdeveloped countries.
This glossary of economics is a list of definitions of terms and concepts used in economics, its sub-disciplines, and related fields.