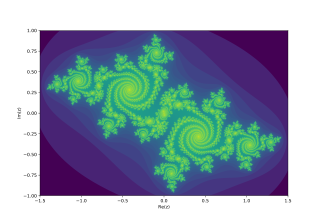
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.
In complex dynamics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

In geometry, a locus is a set of all points, whose location satisfies or is determined by one or more specified conditions.
Complex dynamics, or holomorphic dynamics, is the study of dynamical systems obtained by iterating a complex analytic mapping. This article focuses on the case of algebraic dynamics, where a polynomial or rational function is iterated. In geometric terms, that amounts to iterating a mapping from some algebraic variety to itself. The related theory of arithmetic dynamics studies iteration over the rational numbers or the p-adic numbers instead of the complex numbers.
This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor. Rössler interpreted it as a formalization of a taffy-pulling machine.

The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial p(z) ∈ [z] or transcendental function. It is the Julia set of the meromorphic function z ↦ z − p(z)/p′(z) which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, k = 1, …, deg(p). In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.
In mathematics, the rotation number is an invariant of homeomorphisms of the circle.
In mathematics, a de Rham curve is a continuous fractal curve obtained as the image of the Cantor space, or, equivalently, from the base-two expansion of the real numbers in the unit interval. Many well-known fractal curves, including the Cantor function, Cesàro–Faber curve, Minkowski's question mark function, blancmange curve, and the Koch curve are all examples of de Rham curves. The general form of the curve was first described by Georges de Rham in 1957.
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray.
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.
In mathematics, an orbit portrait is a combinatorial tool used in complex dynamics for understanding the behavior of one-complex dimensional quadratic maps.

In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping instead of used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.
The filled-in Julia set of a polynomial is a Julia set and its interior, non-escaping set.
A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers.
Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Part of the inspiration comes from complex dynamics, the study of the iteration of self-maps of the complex plane or other complex algebraic varieties. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.

A Douady rabbit is a fractal derived from the Julia set of the function , when parameter is near the center of one of the period three bulbs of the Mandelbrot set for a complex quadratic map.

In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component where the rational function is conformally conjugate to an irrational rotation of the standard annulus.
A vortex sheet is a term used in fluid mechanics for a surface across which there is a discontinuity in fluid velocity, such as in slippage of one layer of fluid over another. While the tangential components of the flow velocity are discontinuous across the vortex sheet, the normal component of the flow velocity is continuous. The discontinuity in the tangential velocity means the flow has infinite vorticity on a vortex sheet.

There are many programs and algorithms used to plot the Mandelbrot set and other fractals, some of which are described in fractal-generating software. These programs use a variety of algorithms to determine the color of individual pixels efficiently.