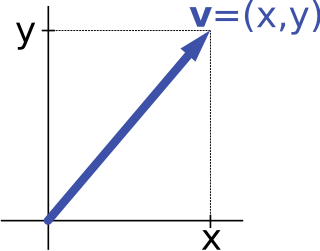In engineering and science, dimensional analysis is the analysis of the relationships between different physical quantities by identifying their base quantities and units of measurement and tracking these dimensions as calculations or comparisons are performed. The term dimensional analysis is also used to refer to conversion of units from one dimensional unit to another, which can be used to evaluate scientific formulae.

In mathematics, Hausdorff dimension is a measure of roughness, or more specifically, fractal dimension, that was introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computation of dimensions for highly irregular or "rough" sets, this dimension is also commonly referred to as the Hausdorff–Besicovitch dimension.

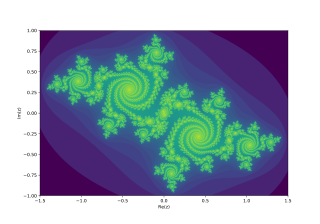
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bound in absolute value.

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering of the class of objects to which it belongs. Magnitude as a concept dates to Ancient Greece and has been applied as a measure of distance from one object to another. For numbers, the absolute value of a number is commonly applied as the measure of units between a number and zero.

The Buddhabrot is the probability distribution over the trajectories of points that escape the Mandelbrot fractal. Its name reflects its pareidolic resemblance to classical depictions of Gautama Buddha, seated in a meditation pose with a forehead mark (tikka), a traditional oval crown (ushnisha), and ringlet of hair.

Pickover stalks are certain kinds of details to be found empirically in the Mandelbrot set, in the study of fractal geometry. They are so named after the researcher Clifford Pickover, whose "epsilon cross" method was instrumental in their discovery. An "epsilon cross" is a cross-shaped orbit trap.

The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial p(Z) ∈ ℂ[Z] or transcendental function. It is the Julia set of the meromorphic function z ↦ z − p(z)/p′(z) which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, k = 1, …, deg(p). In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.

The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:
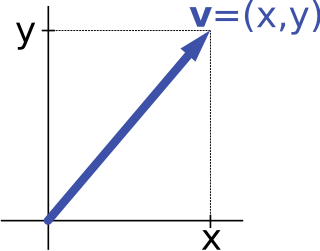
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.

In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping instead of used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.
The filled-in Julia set of a polynomial is a Julia set and its interior, non-escaping set

In mathematics, a Multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions. The name is a portmanteau of multiple and Mandelbrot set. The same can be applied to the Julia set, this being called Multijulia set.

The Mandelbulb is a three-dimensional fractal, constructed for the first time in 1997 by Jules Ruis and in 2009 further developed by Daniel White and Paul Nylander using spherical coordinates.
Space-filling trees are geometric constructions that are analogous to space-filling curves, but have a branching, tree-like structure and are rooted. A space-filling tree is defined by an incremental process that results in a tree for which every point in the space has a finite-length path that converges to it. In contrast to space-filling curves, individual paths in the tree are short, allowing any part of the space to be quickly reached from the root. The simplest examples of space-filling trees have a regular, self-similar, fractal structure, but can be generalized to non-regular and even randomized/Monte-Carlo variants. Space-filling trees have interesting parallels in nature, including fluid distribution systems, vascular networks, and fractal plant growth, and many interesting connections to L-systems in computer science.

In mathematics, an orbit trap is a method of colouring fractal images based upon how close an iterative function, used to create the fractal, approaches a geometric shape, called a "trap". Typical traps are points, lines, circles, flower shapes and even raster images. Orbit traps are typically used to colour two dimensional fractals representing the complex plane.

There are many programs and algorithms used to plot the Mandelbrot set and other fractals, some of which are described in fractal-generating software. These programs use a variety of algorithms to determine the color of individual pixels efficiently.