In mathematics, an orbit trap is a method of colouring fractal images based upon how close an iterative function, used to create the fractal, approaches a geometric shape, called a "trap". Typical traps are points, lines, circles, flower shapes and even raster images. Orbit traps are typically used to colour two dimensional fractals representing the complex plane.
A point-based orbit trap colours a point based upon how close a function's orbit comes to a single point, typically the origin.
A line-based orbit trap colours a point based upon how close a function's orbit comes to one or more lines, typically vertical or horizontal (x=a or y=a lines). Pickover stalks are an example of a line based orbit trap which use two lines.
Orbit traps are typically used with the class of two-dimensional fractals based on an iterative function. A program that creates such a fractal colours each pixel, which represent discrete points in the complex plane, based upon the behaviour of those points when they pass through a function a set number of times.
The best known example of this kind of fractal is the Mandelbrot set, which is based upon the function zn+1 = zn2 + c. The most common way of colouring Mandelbrot images is by taking the number of iterations required to reach a certain bailout value and then assigning that value a colour. This is called the escape time algorithm.
A program that colours the Mandelbrot set using a point-based orbit trap will assign each pixel with a “distance” variable, that will typically be very high when first assigned:
doubledistance=10e5As the program passes the complex value through the iterative function it will check the distance between each point in the orbit and the trap point. The value of the distance variable will be the shortest distance found during the iteration:
privatedoublegetDistance(Complexc,Complexpoint,intmaxIteration){doubledistance=1e20;Complexz=newComplex(0,0);for(inti=0;i<maxIteration;i++){// Perform Mandelbrot iterationz=z.multiply(z);z=z.add(c);// Set new distance dist = min( dist, |z-point| )ComplexzMinusPoint=newComplex(z);zMinusPoint=zMinusPoint.subtract(point);doublezMinusPointModulus=zMinusPoint.magnitude();if(zMinusPointModulus<distance)distance=zMinusPointModulus;}returndistance;}
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.
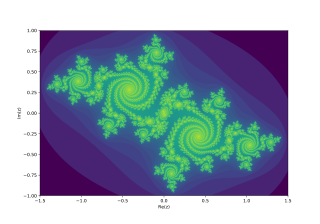
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.
Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.
The Buddhabrot is the probability distribution over the trajectories of points that escape the Mandelbrot fractal. Its name reflects its pareidolic resemblance to classical depictions of Gautama Buddha, seated in a meditation pose with a forehead mark (tikka), a traditional oval crown (ushnisha), and ringlet of hair.
Pickover stalks are certain kinds of details to be found empirically in the Mandelbrot set, in the study of fractal geometry. They are so named after the researcher Clifford Pickover, whose "epsilon cross" method was instrumental in their discovery. An "epsilon cross" is a cross-shaped orbit trap.
The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial p(Z) ∈ ℂ[Z] or transcendental function. It is the Julia set of the meromorphic function z ↦ z − p(z)/p′(z) which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, k = 1, …, deg(p). In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.
The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set. Although this curve is only rarely a half-line (ray) it is called a ray because it is an image of a ray.
The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve–like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension. Although the "paradox of length" was previously noted by Hugo Steinhaus, the first systematic study of this phenomenon was by Lewis Fry Richardson, and it was expanded upon by Benoit Mandelbrot.
In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping instead of used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.
The concept of Misiurewicz point is a topic in the field of mathematics. It refers to a specific parameter value in the Mandelbrot set and real quadratic maps of the interval, where the critical point becomes periodic after a finite number of iterations, but it is not periodic itself. The term is also used for parameters in a multibrot set where the unique critical point is strictly pre-periodic. It is worth noting that this term may not make much sense for maps that have more than one free critical point. Michał Misiurewicz, a Polish-American mathematician, was the first one to study these points, and they are named after him. The Principal Misiurewicz point of the wake 1/31 is an example of such a point.
The filled-in Julia set of a polynomial is a Julia set and its interior, non-escaping set
A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers.
In mathematics, a Multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions. The name is a portmanteau of multiple and Mandelbrot set. The same can be applied to the Julia set, this being called Multijulia set.
Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics.
In mathematics, the mandelbox is a fractal with a boxlike shape found by Tom Lowe in 2010. It is defined in a similar way to the famous Mandelbrot set as the values of a parameter such that the origin does not escape to infinity under iteration of certain geometrical transformations. The mandelbox is defined as a map of continuous Julia sets, but, unlike the Mandelbrot set, can be defined in any number of dimensions. It is typically drawn in three dimensions for illustrative purposes.
In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component where the rational function is conformally conjugate to an irrational rotation of the standard annulus.
There are many programs and algorithms used to plot the Mandelbrot set and other fractals, some of which are described in fractal-generating software. These programs use a variety of algorithms to determine the color of individual pixels efficiently.