In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

In computing, floating-point arithmetic (FP) is arithmetic that represents subsets of real numbers using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. Numbers of this form are called floating-point numbers. For example, 12.345 is a floating-point number in base ten with five digits of precision:
IEEE 754-1985 is a historic industry standard for representing floating-point numbers in computers, officially adopted in 1985 and superseded in 2008 by IEEE 754-2008, and then again in 2019 by minor revision IEEE 754-2019. During its 23 years, it was the most widely used format for floating-point computation. It was implemented in software, in the form of floating-point libraries, and in hardware, in the instructions of many CPUs and FPUs. The first integrated circuit to implement the draft of what was to become IEEE 754-1985 was the Intel 8087.

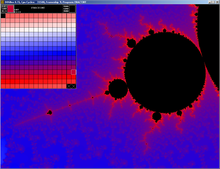
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.

x86 is a family of complex instruction set computer (CISC) instruction set architectures initially developed by Intel based on the 8086 microprocessor and its 8-bit-external-bus variant, the 8088. The 8086 was introduced in 1978 as a fully 16-bit extension of 8-bit Intel's 8080 microprocessor, with memory segmentation as a solution for addressing more memory than can be covered by a plain 16-bit address. The term "x86" came into being because the names of several successors to Intel's 8086 processor end in "86", including the 80186, 80286, 80386 and 80486. Colloquially, their names were "186", "286", "386" and "486".

A floating-point unit (FPU), numeric processing unit (NPU), colloquially math coprocessor, is a part of a computer system specially designed to carry out operations on floating-point numbers. Typical operations are addition, subtraction, multiplication, division, and square root. Some FPUs can also perform various transcendental functions such as exponential or trigonometric calculations, but the accuracy can be low, so some systems prefer to compute these functions in software.

Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.

MMX is a single instruction, multiple data (SIMD) instruction set architecture designed by Intel, introduced on January 8, 1997 with its Pentium P5 (microarchitecture) based line of microprocessors, named "Pentium with MMX Technology". It developed out of a similar unit introduced on the Intel i860, and earlier the Intel i750 video pixel processor. MMX is a processor supplementary capability that is supported on IA-32 processors by Intel and other vendors as of 1997. AMD also added MMX instruction set in its K6 processor.

A coprocessor is a computer processor used to supplement the functions of the primary processor. Operations performed by the coprocessor may be floating-point arithmetic, graphics, signal processing, string processing, cryptography or I/O interfacing with peripheral devices. By offloading processor-intensive tasks from the main processor, coprocessors can accelerate system performance. Coprocessors allow a line of computers to be customized, so that customers who do not need the extra performance do not need to pay for it.
The Atari Microsoft BASIC and Atari Microsoft BASIC II variants of the 6502-version of Microsoft BASIC ported to the Atari 8-bit computers. The first version, released 1981, required 32 KB of RAM and was supplied on floppy disk. The second version, released the next year, had most of the code on a ROM cartridge with additional functions on an optional floppy.
In computer science, arbitrary-precision arithmetic, also called bignum arithmetic, multiple-precision arithmetic, or sometimes infinite-precision arithmetic, indicates that calculations are performed on numbers whose digits of precision are potentially limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most arithmetic logic unit (ALU) hardware, which typically offers between 8 and 64 bits of precision.

The Intel 8087, announced in 1980, was the first floating-point coprocessor for the 8086 line of microprocessors. The purpose of the chip was to speed up floating-point arithmetic operations, such as addition, subtraction, multiplication, division, and square root. It also computes transcendental functions such as exponential, logarithmic or trigonometric calculations. The performance enhancements were from approximately 20% to over 500%, depending on the specific application. The 8087 could perform about 50,000 FLOPS using around 2.4 watts.

RapidCAD is a specially packaged Intel 486DX and a dummy floating point unit (FPU) designed as pin-compatible replacements for an Intel 80386 processor and 80387 FPU. Because the i486DX has a working on-chip FPU, a dummy FPU package is supplied to go in the Intel 387 FPU socket. The dummy FPU is used to provide the FERR signal, necessary for compatibility purposes.
x87 is a floating-point-related subset of the x86 architecture instruction set. It originated as an extension of the 8086 instruction set in the form of optional floating-point coprocessors that work in tandem with corresponding x86 CPUs. These microchips have names ending in "87". This is also known as the NPX. Like other extensions to the basic instruction set, x87 instructions are not strictly needed to construct working programs, but provide hardware and microcode implementations of common numerical tasks, allowing these tasks to be performed much faster than corresponding machine code routines can. The x87 instruction set includes instructions for basic floating-point operations such as addition, subtraction and comparison, but also for more complex numerical operations, such as the computation of the tangent function and its inverse, for example.
Extended precision refers to floating-point number formats that provide greater precision than the basic floating-point formats. Extended precision formats support a basic format by minimizing roundoff and overflow errors in intermediate values of expressions on the base format. In contrast to extended precision, arbitrary-precision arithmetic refers to implementations of much larger numeric types using special software.

Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics.

In mathematics, an orbit trap is a method of colouring fractal images based upon how close an iterative function, used to create the fractal, approaches a geometric shape, called a "trap". Typical traps are points, lines, circles, flower shapes and even raster images. Orbit traps are typically used to colour two dimensional fractals representing the complex plane.

Ultra Fractal is a fractal generation and rendering software application. The program was the first publicly available fractal software which featured layering methods previously only found in image editing software. Because of this, the program has become popular for use in the creation of fractal art.
asm.js is a subset of JavaScript designed to allow computer software written in languages such as C to be run as web applications while maintaining performance characteristics considerably better than standard JavaScript, which is the typical language used for such applications.

Kalles Fraktaler is a free Windows-based fractal zoom computer program used for zooming into fractals such as the Mandelbrot set and the Burning Ship fractal at very high speed, utilizing Perturbation and Series Approximation.