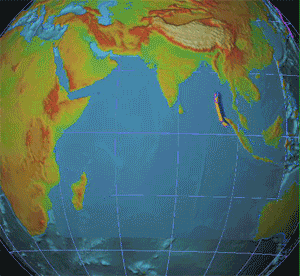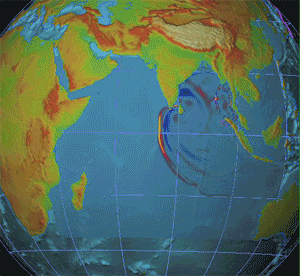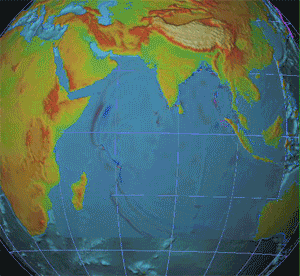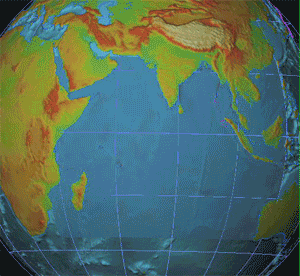
Seismology is the scientific study of earthquakes and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions.

In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats. In other words, it is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings. Wavelength is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter lambda (λ). The term "wavelength" is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.

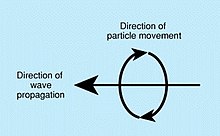
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Periodic waves oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero.

A seismic wave is a mechanical wave of acoustic energy that travels through the Earth or another planetary body. It can result from an earthquake, volcanic eruption, magma movement, a large landslide and a large man-made explosion that produces low-frequency acoustic energy. Seismic waves are studied by seismologists, who record the waves using seismometers, hydrophones, or accelerometers. Seismic waves are distinguished from seismic noise, which is persistent low-amplitude vibration arising from a variety of natural and anthropogenic sources.

Longitudinal waves are waves in which the vibration of the medium is parallel to the direction the wave travels and displacement of the medium is in the same direction of the wave propagation. Mechanical longitudinal waves are also called compressional or compression waves, because they produce compression and rarefaction when travelling through a medium, and pressure waves, because they produce increases and decreases in pressure. A wave along the length of a stretched Slinky toy, where the distance between coils increases and decreases, is a good visualization. Real-world examples include sound waves and seismic P-waves.

The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. More simply, the speed of sound is how fast vibrations travel. At 20 °C (68 °F), the speed of sound in air is about 343 m/s, or 1 km in 2.91 s or one mile in 4.69 s. It depends strongly on temperature as well as the medium through which a sound wave is propagating.
Seismic tomography or seismotomography is a technique for imaging the subsurface of the Earth using seismic waves. The properties of seismic waves are modified by the material through which they travel. By comparing the differences in seismic waves recorded at different locations, it is possible to create a model of the subsurface structure. Most commonly, these seismic waves are generated by earthquakes or man-made sources such as explosions. Different types of waves, including P, S, Rayleigh, and Love waves can be used for tomographic images, though each comes with their own benefits and downsides and are used depending on the geologic setting, seismometer coverage, distance from nearby earthquakes, and required resolution. The model created by tomographic imaging is almost always a seismic velocity model, and features within this model may be interpreted as structural, thermal, or compositional variations. Geoscientists apply seismic tomography to a wide variety of settings in which the subsurface structure is of interest, ranging in scale from whole-Earth structure to the upper few meters below the surface.

In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the fetch. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over 30 m (100 ft) high, being limited by wind speed, duration, fetch, and water depth.

A P wave is one of the two main types of elastic body waves, called seismic waves in seismology. P waves travel faster than other seismic waves and hence are the first signal from an earthquake to arrive at any affected location or at a seismograph. P waves may be transmitted through gases, liquids, or solids.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.

In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves are a type of elastic wave and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves.
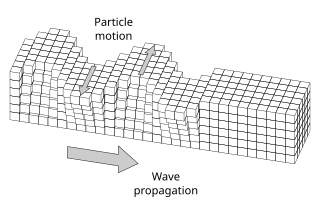
In elastodynamics, Love waves, named after Augustus Edward Hough Love, are horizontally polarized surface waves. The Love wave is a result of the interference of many shear waves (S-waves) guided by an elastic layer, which is welded to an elastic half space on one side while bordering a vacuum on the other side. In seismology, Love waves (also known as Q waves (Quer: German for lateral)) are surface seismic waves that cause horizontal shifting of the Earth during an earthquake. Augustus Edward Hough Love predicted the existence of Love waves mathematically in 1911. They form a distinct class, different from other types of seismic waves, such as P-waves and S-waves (both body waves), or Rayleigh waves (another type of surface wave). Love waves travel with a lower velocity than P- or S- waves, but faster than Rayleigh waves. These waves are observed only when there is a low velocity layer overlying a high velocity layer/ sub–layers.

Lamb waves propagate in solid plates or spheres. They are elastic waves whose particle motion lies in the plane that contains the direction of wave propagation and the direction perpendicular to the plate. In 1917, the English mathematician Horace Lamb published his classic analysis and description of acoustic waves of this type. Their properties turned out to be quite complex. An infinite medium supports just two wave modes traveling at unique velocities; but plates support two infinite sets of Lamb wave modes, whose velocities depend on the relationship between wavelength and plate thickness.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
A seismic metamaterial, is a metamaterial that is designed to counteract the adverse effects of seismic waves on artificial structures, which exist on or near the surface of the Earth. Current designs of seismic metamaterials utilize configurations of boreholes, trees or proposed underground resonators to act as a large scale material. Experiments have observed both reflections and bandgap attenuation from artificially induced seismic waves. These are the first experiments to verify that seismic metamaterials can be measured for frequencies below 100 Hz, where damage from Rayleigh waves is the most harmful to artificial structures.
In geophysics, geology, civil engineering, and related disciplines, seismic noise is a generic name for a relatively persistent vibration of the ground, due to a multitude of causes, that is often a non-interpretable or unwanted component of signals recorded by seismometers.

Seismic inversion involves the set of methods which seismologists use to infer properties through physical measurements. Surface-wave inversion is the method by which elastic properties, density, and thickness of layers in the subsurface are obtained through analysis of surface-wave dispersion. The entire inversion process requires the gathering of seismic data, the creation of dispersion curves, and finally the inference of subsurface properties.
Ground vibrations is a technical term that is being used to describe mostly man-made vibrations of the ground, in contrast to natural vibrations of the Earth studied by seismology. For example, vibrations caused by explosions, construction works, railway and road transport, etc. - all belong to ground vibrations.
In seismology, an earthquake rupture is the extent of slip that occurs during an earthquake in the Earth's crust. Earthquakes occur for many reasons that include: landslides, movement of magma in a volcano, the formation of a new fault, or, most commonly of all, a slip on an existing fault.
Brillouin spectroscopy is an empirical spectroscopy technique which allows the determination of elastic moduli of materials. The technique uses inelastic scattering of light when it encounters acoustic phonons in a crystal, a process known as Brillouin scattering, to determine phonon energies and therefore interatomic potentials of a material. The scattering occurs when an electromagnetic wave interacts with a density wave, photon-phonon scattering.