Bayesian probability is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectation representing a state of knowledge or as quantification of a personal belief.

Probability is the branch of mathematics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur. The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2.
The word probability has been used in a variety of ways since it was first applied to the mathematical study of games of chance. Does probability measure the real, physical, tendency of something to occur, or is it a measure of how strongly one believes it will occur, or does it draw on both these elements? In answering such questions, mathematicians interpret the probability values of probability theory.

Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.

Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
The following outline is provided as an overview of and topical guide to statistics:

A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently support a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a p-value computed from the test statistic. Roughly 100 specialized statistical tests have been defined.
The likelihood function is the joint probability mass of observed data viewed as a function of the parameters of a statistical model. Intuitively, the likelihood function is the probability of observing data assuming is the actual parameter.
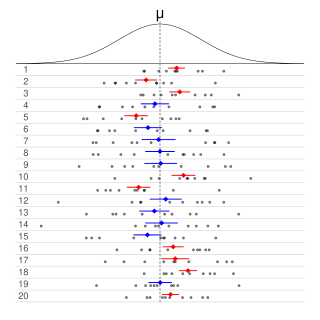
Informally, in frequentist statistics, a confidence interval (CI) is an interval which is expected to typically contain the parameter being estimated. More specifically, given a confidence level , a CI is a random interval which contains the parameter being estimated % of the time. The confidence level, degree of confidence or confidence coefficient represents the long-run proportion of CIs that theoretically contain the true value of the parameter; this is tantamount to the nominal coverage probability. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value.
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability, where probability expresses a degree of belief in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation, which views probability as the limit of the relative frequency of an event after many trials. More concretely, analysis in Bayesian methods codifies prior knowledge in the form of a prior distribution.

In probability theory, inverse probability is an old term for the probability distribution of an unobserved variable.
The classical definition or interpretation of probability is identified with the works of Jacob Bernoulli and Pierre-Simon Laplace. As stated in Laplace's Théorie analytique des probabilités,
Fiducial inference is one of a number of different types of statistical inference. These are rules, intended for general application, by which conclusions can be drawn from samples of data. In modern statistical practice, attempts to work with fiducial inference have fallen out of fashion in favour of frequentist inference, Bayesian inference and decision theory. However, fiducial inference is important in the history of statistics since its development led to the parallel development of concepts and tools in theoretical statistics that are widely used. Some current research in statistical methodology is either explicitly linked to fiducial inference or is closely connected to it.
Statistics, in the modern sense of the word, began evolving in the 18th century in response to the novel needs of industrializing sovereign states.
Statistics models the collection, organization, analysis, interpretation, and presentation of data. Statistics are also used to solve mathematical problems. Conclusions drawn from statistical analysis typically contain certainties, uncertainties, or the probability of an event occurring. Statistics can be used to predict or classify events based on a large set of data, which is an integral application of statistics in fields such as genomics, economics, bioinformatics, and machine learning.
Frequentist inference is a type of statistical inference based in frequentist probability, which treats “probability” in equivalent terms to “frequency” and draws conclusions from sample-data by means of emphasizing the frequency or proportion of findings in the data. Frequentist inference underlies frequentist statistics, in which the well-established methodologies of statistical hypothesis testing and confidence intervals are founded.
The following is a timeline of probability and statistics.
In statistical inference, the concept of a confidence distribution (CD) has often been loosely referred to as a distribution function on the parameter space that can represent confidence intervals of all levels for a parameter of interest. Historically, it has typically been constructed by inverting the upper limits of lower sided confidence intervals of all levels, and it was also commonly associated with a fiducial interpretation, although it is a purely frequentist concept. A confidence distribution is NOT a probability distribution function of the parameter of interest, but may still be a function useful for making inferences.
Likelihoodist statistics or likelihoodism is an approach to statistics that exclusively or primarily uses the likelihood function. Likelihoodist statistics is a more minor school than the main approaches of Bayesian statistics and frequentist statistics, but has some adherents and applications. The central idea of likelihoodism is the likelihood principle: data are interpreted as evidence, and the strength of the evidence is measured by the likelihood function. Beyond this, there are significant differences within likelihood approaches: "orthodox" likelihoodists consider data only as evidence, and do not use it as the basis of statistical inference, while others make inferences based on likelihood, but without using Bayesian inference or frequentist inference. Likelihoodism is thus criticized for either not providing a basis for belief or action, or not satisfying the requirements of these other schools.




